自然语言处理入门 - 万泽的博客

简介

自然语言处理的可能应用领域有：

机器翻译
自动文摘
信息检索
文档分类
问答系统
信息过滤，信息抽取
文字编辑和自动校对
作文自动评分
语音识别
语音合成，text to speech

信息熵

信息熵是个非常让人难懂的概念，尤其是当你在很多领域都接触到信息熵的概念和各种应用的时候，你会发现你根本就没理解信息熵这个概念。比如自然语言处理领域，信息熵有着非常多的应用，然后自然信息传输领域也有很多应用，信息熵的概念基本上是现在信息论的基石吧。

不管怎么说，我们先死记硬背一下，信息熵的定义，就是一个事物或者一个什么东西吧，在一个系统中出现的几率为p，则这个东西在这个系统中的信息熵为：

$$ H = - p log_2{p} $$

首先从最简单的抛硬币开始吧，对于正面来说出现的几率为1/2，则一次抛硬币你看到正面的信息熵为 0.5，然后反面的信息熵也是0.5 ¹ 。信息熵的单位是bit，然后信息熵服从可加性（也就是总系统的信息熵是各个子系统的信息熵的加和），所以抛一枚硬币，正面和反面的信息熵总和就是 1 bit。从信息论的角度来说就是用一个字节就可以描述抛一枚硬币的可能信息量了。信息论一开始就是专注于信息传输领域的。

所以我们又看到这样一个问题，本问题摘自宗庆成统计自然语言处理第二版例2-3：

假设a,b,c,d,e,f 6个字符出现的概率分别是 1/8 1/4 1/8 1/4 1/8 1/8 ，那么传输一个字符的信息熵为？

传输一个字符 a b c d e f只可能有这六种情况，分别信息熵为：

H = -[1/8log1/8 + 1/4log1/4 + 1/8log1/8 + 1/4log1/4 + 1/8log1/8 + 1/8log1/8] = 2.5 bit

也就是传输这六个字母需要2.5bit，则给三个bit位就完全够用了，然后具体设计一种信息编码规则即可，在设计编码规则的时候还要考虑具体情况出现的概率问题，这里具体细节就不讨论了。总之信息熵一开始就是干这个用的。

如果一个事件一定会发生，那么其信息熵等于0，如果一个事件发生的概率为0，其信息熵也等于0。信息熵为0表示这个事件发送给你并没有为你带来额外的信息。就以抛硬币来描述一个事件，则你对硬币一无所知的时候，信息熵=1为最大信息熵的可能，也就是一半一半0.5的情况。

所以薛定谔的猫在一半生一半的死的情况下打开黑盒子，流出来的信息熵是最大的，或者说流出来的信息量是最多的。

信息增益

信息增益在决策树算法的分类特征选择中很重要，暂时先简单理解为就是引入这个特征分类信息熵增量很大，这样获取这个特征对整个系统确定程度影响最大，或者简单来说就是这个特征好啊，引入之后能够收获更多的信息。

联合熵和条件熵

实际是从概率分布的联合概率和条件概率推出来的概念。而所谓联合概率就是两个事件一起出现的概率；而所谓条件概率就是已知Y已经发生了，X事件发生的概率。

$$ H(X,Y) = - \sum_{x \epsilon X} \sum_{y \epsilon Y} p(x,y)log(p(x,y)) $$

XY的联合熵是描述一对随机变量平均所需要的信息量。

熵的连锁规则：

$$ H(X_1,X_2 ...) = H(X_1) + H(X_2|X_1) + H(X_3| X_1, X_2) $$

也就是多个事件一起出现的信息熵等于第一个事件出现的信息熵加上第一个事件出现了第二个事件再出现的信息熵，以此类推。

互信息

互信息是用来衡量两个事件的相关度的。互信息的定义如下：

$$ I(X;Y) = H(X) - H(X|Y) $$

注意这个分号，如果是逗号，表示两个事件一起出现，如果是|则是Y已经出现了求X的条件概率。

其含义就是X和Y的互信息是知道Y事件之后对X事件发生产生的信息熵的减少量。也就是假设不知道Y事件X事件的信息量=2，而知道Y之后X事件再发生的信息量=1，则X和Y的互信息量=1。

假设XY不相干，则XY的互信息量=0；假设Y事件发生则X事件必发生，则XY的互信息量=X的信息熵。

由熵的链式规则有：

$$ I(X;Y) = H(X) - H(X|Y) = H(X) + H(Y) - H(X,Y) $$

相对熵或者交叉熵

相对熵也被称为交叉熵【似乎相对熵和交叉熵是两个不同的概念，数学之美上的说法存疑。】，这个我们在机器学习核对学习算法的误差是接触过，相对熵是用来两个取值为正数的函数相似性的。

对于两个完全相同的函数，他们的相对熵为0
相对熵越大，两个函数差异越大，反之相对熵越小，两个函数差异越小。
如上所述，相对熵可以用来衡量两个概率分布函数的差异性

互信息就是两个事件的联合分布和独立分布的相对熵，所以两个事件越接近独立分布，则相关性越小，则相对熵越小，则互信息越小；反之两个事件越不接近独立分布，则相关性越大，则相对熵越大，则互信息越大。

统计语言模型

S 表示一连串顺序排列的词语，S在文本中出现的可能性，P(S) ，

利用条件概率：

$$ P(S) = P(word1)P(word2|word1)P(word3|word1word2)...P(wordn|word1word2word3...wordn-1) $$

马尔科夫假设

任何一连串事件序列某个状态发生的概率只依赖于它的前几个状态，这一事件序列叫做马尔科夫链。

如果只依赖于它的前一个词，那么这种模型称为二元模型，也就是一阶马尔科夫链，记作 bigram

如果依赖于它的前两个词，那么这种模型称为三元模型，也就是二阶马尔科夫链，记作 trigram

下面以二元模型为例子，计算一句话出现的概率：

$$ P(S) = P(word1)P(word2|word1)P(word3|word2)...P(wordn|wordn-1) $$

$P(w_i|w_{i-1})$ 是一个词出现之后下一个词出现的条件概率，利用条件概率有：

$$ P(w_i|w_{i-1}) = P(w_iw_{i-1})/P(w_{i-1}) $$

令句首标记为 <BOS> 令句末标记为 <EOS> 。

其中 $P(w_iw_{i-1})$ 的概率就是两个词在整个文本中所占的频率，具体等于目标两个词序列的记数/总文本记数

而 $P(w_{i-1})$ 是前一个词出现的次数/总文本数，最后得到：

$$ P(w_i|w_{i-1}) = 两个词序列计数/前一个词的计数 $$

请参看宗庆成的自然语言处理第二版P85的例子详细理解如何计算一个句子出现的概率的计算方法。

大数定理

在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。

高阶语言模型

上面简单的二元模型只假设一个词只和其前面的那个词相关，如果假设前面的N-1个词和这个词相关，那么这个模型就称为N元模型。

古德-图灵估计

上面的统计一个句子出现概率的计算方法，某些序列在语料库（统计文本）中并没有出现过，或者出现次数极少。这些句子概率的计算都估算为零是不合适的。古德-图灵估计就是来解决这个问题的。

对于没有看见的事件，我们不能认为它发生的概率就是零，因此我们从概率的总量中分配一个很小的比例给予这些没有看见的事件。

基本计算公式是：

$$ N = \sum_1^{\infty}r N_r $$

这个公式含义很明显，就是出现1次（r=1）的词有多少个（$N_r$），逐个相加得到总词数。写成下面的形式会简单一些：

$$ N = 1N_1 + 2N_2 + 3N_3 ... $$

而古德-图灵估计就是假设r次（一般要到非常小的时候才会上这个估计）有如下规律（因为次数低，甚至可能为0所以这里的多少次是未知的）：

$$ r^* N_r = (r+1)N_{r+1} $$

这个公式看起来很突兀，但我们可以这样理解：

$$ N = 2N_2 + 3N_3 + 4N_4 ... $$

也就是出现次数很少的词出现的次数乘以具体那些词的次数大体可以用次数加一，上一次数的情况来估计。因为次数很少，这个公式一直加到无穷大，是可以认为估计损失极小的。

于是对于具体出现 $r^*$ 次的某个词，其出现的概率为：

$$ P_r = \frac{r^*}{N} $$

这种估计方法，还剩下来一个 $1N_1$ ，其就是给未知事件的，未知事件的概率估计为：

$$ P_0 = \frac{N_1}{N} $$

也就是未知事件出现的概率等于出现1次的词的计数除以总词数。

中文分词

自然语言是上下相关的，自然语言研究需要为这种上下文相关的特性建立数学模型，这个数学模型就是人们常说的统计语言模型（Statistical Language Model）。

贾里尼克认为：一个句子是否合理，就看它的可能性大小如何。

这其中有个问题就是如何穷举所有可能的分词方法：这是一个动态规划问题，可以利用维特比算法（Viterbi）来解决这个问题。

总的说来如上面讨论的，基于统计和词典的，来获得一个最大可能性的句子的分词方法，是目前兼顾准确性和性能的最佳方案了，后续很多方法都应该站在其肩膀上，试着更好地解决词典完善和命名实体识别等等问题。

隐马尔科夫模型

广义通信模型

人与人之间的语言，或者其他任何形式的信息交流，都可以看做是一种广义上的通信模型，一个信号编码序列通过某种信息载体在信道中发送出去，然后被接受者接受，并进行转码的过程。

我们需要找到的就是根据观测信号o1 o2 o3... 对应的最大条件概率状态信号 s1 s2 s3... 。【下面公式argmax是一种操作，找到后面表达式的最大值】

$$ s_1, s_2, s_3, \dots = \underset{all s_1,s_2,s3,\dots}{\arg\max} P(s_1,s_2,s_3,\dots | o_1,o_2,o_3,\dots) $$

按照条件概率有：

$$ s_1, s_2, s_3, \dots = \underset{all s_1,s_2,s3,\dots}{\arg\max} \frac{P(s_1,s_2,s_3,\dots) \cdot P( o_1,o_2,o_3,\dots |s_1,s_2,s_3,\dots)}{P(o_1,o_2,o_3,\dots)} $$

因为要求最大值，具体观测信号的发射概率可以忽略：

$$ s_1, s_2, s_3, \dots = \underset{all s_1,s_2,s3,\dots}{\arg\max} P(s_1,s_2,s_3,\dots) \cdot P( o_1,o_2,o_3,\dots |s_1,s_2,s_3,\dots) $$

s1,s2--> o1,o2 的条件概率是状态信息s1...在传输后成为接受者接受的o1...的概率。而 s1,s2...是发送端出现这个随机过程的概率。

这个计算过程可以利用隐马尔科夫模型来计算。

马尔科夫模型

首先是马尔科夫模型，其还是比较简单易懂的。首先从随机过程开始，假设你要研究一个系统，这个系统随机吐出一些信号，s1 s2 ... 具体就是这个系统的某种激活状态。这种随机过程的生成可以用下面的图形来描述：

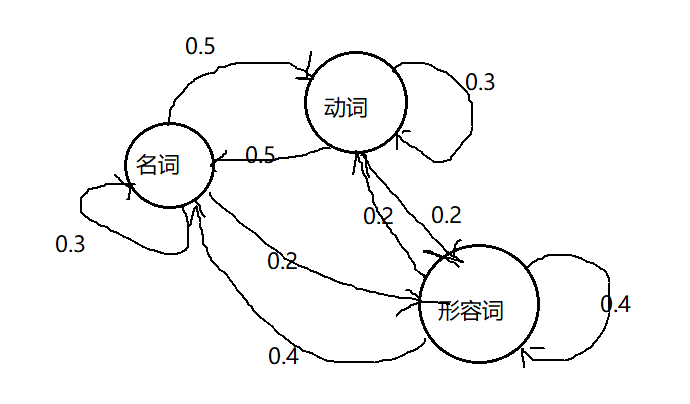
这个例子来自宗庆成统计自然语言处理第二版P109。

一段文字中名词、动词、形容词出现概率可由三个状态的马尔科夫模型描述，这个状态的转移矩阵如下所示【下面矩阵头从左到右和从上到下依次是名词，动词，形容词。】：

$$ \begin{bmatrix}0.3 & 0.5 & 0.2 \ 0.5 & 0.3 & 0.2 \ 0.4 & 0.2 & 0.4\end{bmatrix} $$

假设我们观察到序列 名动形名 ，则这个序列出现的概率为：

$$ P(名)P(动|名)P(形|动)P(名|形) = 0.50.2*0.4 = 0.04 $$

马尔科夫模型其内暗含了这样的假定：其内的随机过程为马尔科夫链过程，状态只受前一个状态影响。

隐马尔科夫模型

隐马尔科夫模型在上面的讨论上，引入这样的东西，那就是我们不能直接观察这个系统的s1 s2 状态，我们只能观察这个而系统抛出来的信号 o1 o2...，这就和之前讨论的广义通信模型有点接近了，也正因为如此隐马尔科夫模型很是通用，即使是后面的条件随机场模型也是站在隐马尔科夫模型的基础上的，因为隐马可夫模型其内有些思想内核是触及了广义通信模型的内核的，而广义通信模型几乎可以用来看待一些信息传输问题，包括自然语言，人的沟通交流也可以看做一种信息传输过程（我们也可以想象，人和机器语言若存在某种人机交互，那么也是符合这个广义通信模型的）。

而隐马尔科夫模型又说我们观察到的 o1 o2 ... 是和这个系统的状态 s1 s2相关的，这是自然。继而隐马尔科夫模型应用马尔科夫链过程简单模型做了如下假定：o1只和最近的s1相关，o2只和最近的s2相关。

我们看到隐马尔可夫模型大方向是没问题的，就是引入马尔科夫链对状态的前后相关性做了太多的简化，这个后面条件随机场模型会进一步完善。

上面讨论的马尔科夫模型引入了状态转移矩阵，然后这个系统启动还需要一个起始状态，在隐马尔可夫模型这里的讨论引入了混淆矩阵 的概念。混淆矩阵描述了隐状态s和输出信号o之间的概率关系。

根据观察序列生成模型

jieba分词的HMM模型数据是直接统计得到的，并没有用到前向-后向算法。具体是BMES四个隐藏状态：

B 标注本字的位置是一个词开始
M 标注本字的位置是一个词的中间
E 标注本字的位置是一个词的结束
S 标注本字是单独成词

先把训练文本整成这样的输入序列：

[('“', 'S'), ('人', 'B'), ('们', 'E'), ('常', 'S'), ('说', 'S'), ('生', 'B'), ('活', 'E'), ('是', 'S'), ('一', 'S'), ('部', 'S'), ('教', 'B'), ('科', 'M'), ('书', 'E'), ('，', 'S'), ('而', 'S'), ('血', 'S'), ('与', 'S'), ('火', 'S'), ('的', 'S'), ('战', 'B'), ('争', 'E'), ('更', 'S'), ('是', 'S'), ('不', 'B'), ('可', 'M'), ('多', 'M'), ('得', 'E'), ('的', 'S'), ('教', 'B'), ('科', 'M'), ('书', 'E'), ('，', 'S'), ('她', 'S'), ('确', 'B'), ('实', 'E'), ('是', 'S'), ('名', 'B'), ('副', 'M'), ('其', 'M'), ('实', 'E'), ('的', 'S'), ('‘', 'S'), ('我', 'S'), ('的', 'S'), ('大', 'B'), ('学', 'E'), ('’', 'S'), ('。', '....

然后整成二元组：

[(('“', 'S'), ('人', 'B')), (('人', 'B'), ('们', 'E')), (('们', 'E'), ('常', 'S')), (('常', 'S'), ('说', 'S')), (('说', 'S'), ('生', 'B')), (('生', 'B'), ('活', 'E')), (('活', 'E'), ('是', 'S')), (('是', 'S'), ('一', 'S')), (('一', 'S'), ('部', 'S')), (('部', 'S'), ('教', 'B')), (('教', 'B'), ('科', 'M')), (('科', 'M'), ('书', 'E')),......

对这个二元组进行统计分析，第一个为因，第二个为果。

状态转移矩阵就是分析第一因BMES到第二果BMES的条件概率。比如说 P(E|B) = P(BE)/ P(B) = C(BE)/C(B) ，也就是统计BE这个序列出现的次数除以第一因为B出现的次数。

发射矩阵就是分析第一因BMES到第二果具体某个字符的条件概率。

更深入的了解读者请参见我编写的 fenci项目hmm文件夹下的train_hmm.py脚本。

维特比算法

条件随机场

条件随机场算是现在实际广泛应用中的一个算法了，其基于HMM隐马尔可夫模型。

参考资料

数学之美第二版吴军著
统计自然语言处理第二版宗成庆
52nlp上关于hmm的教程

脚注

请读者参看知乎这里 maxdeath的讨论。 ↩