统计学学习笔记

目录
首发于：
最近更新于：
分类： archived

均值中位数众数

  • mean 也就是均值，也就是算术平均数，也就是大家熟知的把所有的数加起来然后除以个数，看看这些数平均有多大。
  • median 中位数，是这样的概念：如果我们把一组数从小到大排列，然后最中间的那个数就是中位数。其中最中间的解释是，如果一共有奇数个数字，那么去掉一个最小去掉一个最大，这样类推，最后剩下来的那个数就是中位数；如果一共有偶数个数字，那么最后会剩下两个数字，而中位数就是最后这两个数字的均值。
  • mode 众数，也就是这一组数中出现频率最高或者说分布最多的数。比如说[1,2,2,3]这样一个样本，其中数字2出现次数最多，我们就说这个样本的众数为2。

统计意义

平均值的概念是大家最熟悉的，其是最基本的统计学手段。比如物理学上的测量，为了精确总是需要多次测量取平均值。再比如我们衡量某一类数据的大致平均情况，比如你的考试平均成绩，通过这个平均成绩可以大致得到你对待本学期学业的态度等。

中位数和均值一样也能考察样本总体存在状态，不过区别是中位数对一些极值（特殊的偏离特别远的值）不敏感。以收入来举例子：某些人的收入特别的高，那么如果你用均值来考察社会的收入水平就会有抬高的嫌疑。因为不同的家庭之间的收入并没有共享，但是你在计算中却一并考虑了。这个时候用中位数来考察能更加合理地看着社会总体的收入水平。因此考察家庭平均收入要用中位数。

众数只关注出现次数最多的数，严格来讲其并不具有考察样本总体存在状态的能力了，不过在某些情况下却可以。比如说你头发的颜色这样的定性描述，用众数就很合适。

python相关

自python3.4起，python加入了statistics模块了，所以我们不需要重复发明轮子了。上面的mean，median和mode这三个名字在statistics模块中都是对应的函数，下面是一些演示例子：

from statistics import mean,mode,median

>>> lst = [23,29,20,32,23,21,33,25]
>>> mean(lst)
25.75
>>> median(lst)
24.0
>>> mode(lst)
23

这三个函数都接受一个可迭代对象，然后进行相关操作，如果是空数据，那么将raise statistics.StatisticsError 。

值得注意的是mode还可以操作字符串：

>>> mode(['a','b','a','c','d'])
'a'

然后mode函数并不能处理几个数都是频率最高的情况，比如运行下面命令，将raise statistics.StatisticsError 。

>>> lst = [1,1,2,3,3]
>>> mode(lst)

我们可以利用collections模块的Counter类的most_common方法来获得更健壮的mode函数。

from collections import Counter

def mode(obj):
    """
    多个可能的情况
    """

    c = Counter(obj)

    most = 0
    first = True
    for k,v in c.most_common():
        if first:
            most = v
            first = False
            yield k
        else:
            if most == v:
                yield k
            else:
                break

python3的 statistics 内置模块进行 均值 中位数 和 众数的运算，还是存在一些问题的，python2没有那个模块就不说了，其次就是没有考虑矢量思维和计算效率问题。好了，numpy 和 scipy 出场了。

  1. 首先我们需要把python的可迭代对象（Iterable）变成numpy的ndarray对象，然后如果已经是了，就pass掉。
  2. 然后就是利用numpy和scipy的函数支持了。
import numpy as np
from collections import Iterable

def to_ndarray(pyobj, dtype=None):
    if not isinstance(pyobj, Iterable):
        raise TypeError('it is not a iterable object')

    if isinstance(pyobj, np.ndarray):
        return pyobj

    if dtype is not None:
        return np.array(pyobj, dtype)
    else:
        return np.array(pyobj)


def mean(obj):
    obj = to_ndarray(obj)
    return obj.mean()

def median(obj, axis=None):
    obj = to_ndarray(obj)
    return np.median(obj, axis=axis)

mode统计频数在scipy那里是有个 scipy.stats.mode 函数，不过其只是返回出现频数最大的那个，而且如果最大的频数有多个相同的情况也只返回一个。

方差和标准差

首先来说总体的情况，总体均值是 $\mu$ ，而总体方差具体公式如下所示:

$$ {\sigma }^{2 } =\frac { 1 }{n } \sum _{ i=1 }^{ n }{( X_i - \mu)^2} $$
也就是总体方差是每一个数和总体均值的差的平方和的均值。

>>> from statistics import *
>>> pvariance([0,0,5,5])
6.25

statistics.pvariance(data, mu=None)

如上所示，pvariance还可以接受 mu 可选参数，也就是总体均值，这样可以避免重复计算，若没有赋值则函数会自动计算。

然后总体标准差就是总体方差的平方根，或者说就是上面的 $\sigma$ 。

>>> from statistics import *
>>> pstdev([0,0,5,5])
2.5

pstdev（Population standard deviation）同样还可以接受 mu 可选参数。

在实际应用中，绝大多数情况都是考察的样本而不是总体，所以更常用的是样本方差:

$$ {S }^{2 } =\frac { 1 }{n-1 } \sum _{ i=1 }^{ n }{( X_i - \overline { X } )^2} $$
你可能已经注意到了，上面的是 $n-1$ 而不是 $n$ ，这其中有些统计学的考虑，什么无偏估计，也就是用样本来评估总体的方差的时候，总会估计值偏小，然后再加上一个额外的数据量来让估计值更准确些，大体就是这样，至于具体为何是 n-1 ，那就是统计学里面的高级内容了，总之就是为了更好的估计（从样本估计总体）。

python中的样本方差是 variance 函数，样本标准差是 stdev 函数:

>>> variance([0,0,5,5])
8.333333333333334
>>> stdev([0,0,5,5])
2.886751345948129
>>>

统计意义

方差是来描述数据集的离散程度的，标准差就是方差的平方根，当然同样可以用来描述数据集的离散程度。标准差和实际数据会更一致，比如说统计一班的身高的标准差是 10cm ，这样可以给人一个直观的感受。然后在正态分布中有 均值 $ \pm $ 三个标准差，那么样本中大约 99点几的数据都包含在内了。

简单来说，总体就是整个你要考察的对象，即使是对于上面简单的均值，中位数，众数等等描述性概念，对于总体来说通常都是很难全部考察的。于是我们从总体中取出某一些考察对象（理论上要求是近似于完全的随机取样），然后组成一个样本。然后我们希望对于样本的一些统计描述性数据能够很好地反应总体的数据存在状况。这样所有统计学量实际上都有两种类型，比如均值有总体均值 $\mu$ 和样本均值 $\overline{X}$ 。

python相关

我们还是利用numpy来进行计算：

def pvariance(obj):
    obj = to_ndarray(obj)

    return np.var(obj)

def pstd_deviation(obj):
    obj = to_ndarray(obj)

    return np.std(obj)


def variance(obj):
    obj = to_ndarray(obj)

    return np.var(obj, ddof=1)

def std_deviation(obj):
    obj = to_ndarray(obj)

    return np.std(obj, ddof=1)

注意上面计算样本方差 variance的时候 ddof=1 设置为1，默认是0。在计算样本的时候需要使用样本方差和样本标准差。

中位数和分位数

中位数前面谈过了，就是最中间的那个数。同时还有一种说法是数据集里有 50% 的数比它小，有 百分之50的数比它大。于是分位数的概念由此来了，比如 25% 分位数（quantile）的意思就是在数据集里有 25% 的数比它小。所以如果我们联想到统计学的分布图的话，进而可以把 25%的分位数看作以这个数画一条线，左边的面积是总面积的 25%。

python相关

def quantile(obj, seq=None):
    obj = to_ndarray(obj)

    if seq is None:
        seq = range(0,101,25)

    res = pd.Series(np.percentile(obj, seq), index=seq)
    return res

numpy 里面有 percentile 函数就是分位数 quantile，只是具体要显示要几个分位数位置需要定制。然后上面利用pandas的 Series 数据结构返回，好说明清楚具体是那个分位数。

极差 中程数

极差（range）就是这一组数的最大值和最小值的差值。中程数（midrange）就是这一组数的最大值和最小值的均值。

python相关

因为极差range这个名字和python语言的range函数相冲突，所以python并没有为极差定义一个函数，由于计算公式较简单，我们也不需要额外定义一个公式。就是：

max(lst) - min(lst)

而中程数就是

(max(lst) + min(lst))/2

统计意义

极差是统计学上入门级别的粗略的对样本的离散程度的考察，比如一组数不是很分散，都集中在均值附近，那么其极差就会很小，而同样的情况另一组数如果极差更大，那么我们说第二组数离散程度更大。

中程数可以作为如果样本数组离散程度不是很高的话，作为均值的近似快速计算。

标准分

标准分 $z = \frac{x- \mu}{\sigma}$ 标准分是将不同的正态分布映射到一个标准正态分布上的手段，简单来说就是一种将不同均值不同标准差的正态分布标准化的过程，要理解这个过程首先需要理解标准正态分布：

所谓标准正态分布是值均值为0，标准差为1的正态分布。

标准分比较做出的假设就是 目标研究数据集 或者说学生的得分数据集是 正态分布 。所以现在的任务就是比较不同的正态分布。在正态分布中有个规律：

  • 95.45% 的数据位于两个标准差的范围内
  • 99.73% 的数据位于三个标准差的范围内。

（还是要公式来明确获得）

参考同济大学概率论和数理统计第四版一书 p48 引理：

若 X 分布是正态分布，则 $Z = \frac{X-\mu}{\sigma}$ 分布是标准正态分布。嗯，简单看了下数学公式推导，信心足一些了，没问题的。

条件概率

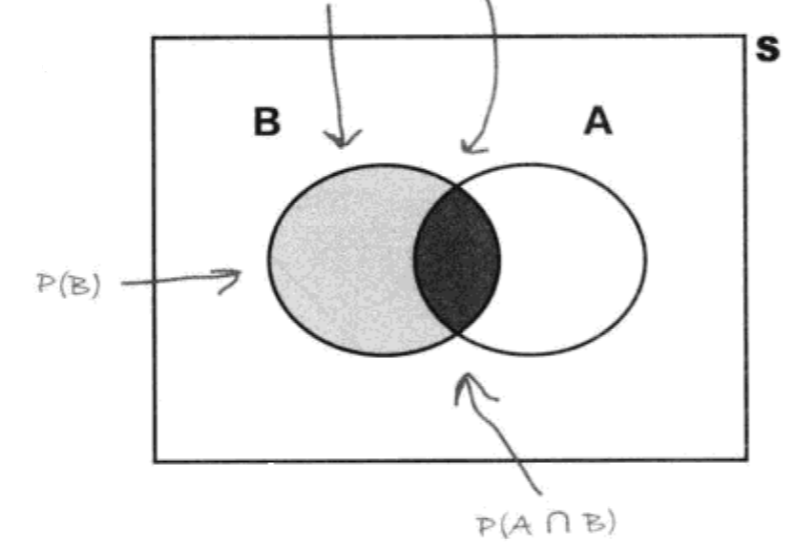
条件概率的维恩图解很有意思：

$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$
用维恩图基本上可以直接写出上面的公式，含义是很明确的。

条件概率

并继而有：

$$ P(A|B) P(B) = P(A \cap B) $$

$$ P(A \cap B) = P(B \cap A) = P(B|A) P(A) $$

用概率树来理解，就是先发生B然后发生A事件，最后事件AB的概率为两个事件的概率乘积，这里我仍然有困惑，AB事件和BA事件两个概率一样吗？（只是针对古典概率模型，到了要考虑顺序的地方人们又使用 P(a,b) 这样的符号，那个时候 P(a,b) 就不等于 P(b,a)。）

互斥事件A，B，即不可能同时发生的事件，则有 $P(A \cap B) =0$

全概率公式：

$$ P(B) = P(A) \times P(B | A) + P(A') \times P(B | A') $$
贝叶斯定理：
$$ P(A|B) = \frac{P(B|A) P(A)}{P(B) = P(A) \times P(B | A) + P(A') \times P(B | A')} $$
贝叶斯定理提供了一个计算逆条件概率的方法，也就是实际情况是先发生 A 再 发生B ，而你想知道B发生之后A发生的概率。

贝叶斯定理思想比上面提及的更深，现在我们假设 A 事件，然后机器或者人针对A事件做了推断 B，我们想知道这个推断B正确的可能性有多大，其中A事件发生的概率，A事件发生后B推断的概率，或者A事件没有发生B推断发生的概率都是从经验数据中可以学习的。而所谓后验就是B推断已经发生了，如果A事件没有发生那么推断错误，如果A事件发生了那么推断正确，所以 $P(A|B)$ 这个也常被统计学家们称为 后验概率，其实际上也就是逆概率，具体计算过程也就是用上面的贝叶斯公式来计算的。

参考资料

  1. 深入浅出统计学
  2. 同济大学 概率论和数理统计
  3. 机器学习 周志华