理解神经网络

学习深度学习不一定要了解神经生物学，对于传统机器学习各个算法也不一定要面面俱到，但对于神经网络基本概念和具体里面矩阵，现在应该升级了，叫做张量运算还是应该有所了解的。

我们来看Keras的30s上手例子：

from keras.models import Sequential

model = Sequential()

from keras.layers import Dense

model.add(Dense(units=64, activation='relu', input_dim=100))
model.add(Dense(units=10, activation='softmax'))

model.compile(loss='categorical_crossentropy',
              optimizer='sgd',
              metrics=['accuracy'])

首先我们需要建立一个模型，最常用的模型是 Sequential 顺序模型。这是最常用的模型。

神经网络现在的发展已经和大脑并无太多关系了，当然早期发展是吸收了一些灵感，所以人们也推荐神经网络应该叫做分层表示学习或者层级表示学习。

注意看上面 layer 就是层的意思，深度学习模型就是层的堆叠。

而上面的Dense 就是我们常说的全连接层。全连接层大概是这样的：

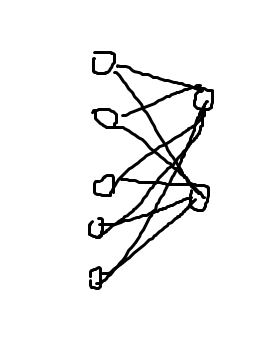
全连接层的意思是本层的每个节点都和后一层的每个节点相连。

Dense的units参数是本层节点数的意思，其也还有一个意思，叫做本层的输出维度数。

每一层神经网络发生了 output = relu(dot(W, input) + b)这样的数学运算。其中 relu 是上面 Dense 指定的 activation 也就是激活函数。我觉得在这里去想神经网络原来那一套并不有助于我们的理解了，反倒是根据数学思维来更方便理解一些。每一层神经网络即这样一层数学运算层，能够对某一个数据集进行了某种线性变换，然后输出另外一个对应的数据集。就如同弗朗索瓦·肖奈所打比方描述的：

一张纸被揉的皱巴巴的，我们可以通过一系列步骤的几何变换，每一步都只是简单的几何变换，但最终完成了某个展平动作，于是我们看到了这张纸上面写着的字。深度学习模型就是解开高纬数据复杂流形的数学机器。

我觉得弗朗索瓦·肖奈的另外一个比方也很好，很形象。可以把深度学习网络看做多级信息的蒸馏操作，信息穿越过滤器，然后纯度越来越高（对任务的帮助越来越大）。

上面公式中 W 是每一层的权重，深度学习训练的过程就是给每一次找到更好的权重参数，从而整个深度学习神经网络能够更好地帮助任务。

model.fit(x_train, y_train, epochs=5, batch_size=32)

训练的过程 x_train 是具体的数据， y_train 是对应的标签数据， epoch 是迭代次数，也就是对于某个训练数据的重复训练次数。batch_size 是一次训练所含样本数，参考了这个网页，因为一次把所有样本训练完开销太大，而每训练一次就算一下损失函数震荡又大，所以现在通用的做法是： mini-batch gradient decent ，小批量数据的梯度下降。这里的batch_size 是一次训练所含的样本数，那么1个epoch就是把所有训练数据都训练完的训练次数是总样本数除以batch_size。

model.compile(loss='categorical_crossentropy',
              optimizer='sgd',
              metrics=['accuracy'])

上面模型在compile的时候需要指定损失函数loss，损失函数是用来衡量模型得到的预测值和真实目标值之间的距离的，简单来说就是损失函数就是给目前模型打分的，来评价模型的效果好坏的。

根据打分来对模型的各个权重参数进行微调使用的是反向传播算法。

反向传播算法

反向传播算法（BP算法 backpropagation）。BP算法先将输入示例提供给输入层神经元，然后信号逐渐向前传递，直到产生输出层结果；然后计算输出层的误差，再将误差逆向传播直隐含层。最后根据隐含层神经元的误差来对连接权重和阈值进行调整的过程。改迭代过程循环进行，直到达到某个条件后停止。

反向传播算法进行调节由优化函数或者说优化器 optimizer来完成。

理解张量

标量向量矩阵一般大家都有所接触了的，张量则是更多的维度的数据结构了。再谈到张量之后我发现之前那些图形几何上的理解的东西最好丢掉，而简单将张量理解为多个维度的数据结构。具体在python程序中就将张量看做numpy模块中的ndarray对象这是没有问题的。

张量的shape

首先看下矩阵方面的情况：

(1,3）这是一个行矢量， for example: [1,2,3]
(3,1) 这是一个列矢量，for example：

$$ \begin{bmatrix} 1\ 2\ 3 \end{bmatrix} $$

(2,3) 表示两行三列

小维度情况带上几何思维这没有问题，但到张量了比如说 shape (3,3,2,3) ，那么最好的理解是这个张量数据有四个维度，其中第一个维度的数据容量是3个，第二个维度的数据容量也是3个。

ndarray对象有这样的索引语法 ndarray[x, y , z] ，其中每一个维度也支持 ndarray[x1:x2, : , :] start:end 这样的语法。这样从维度来理解，就是第一个维度选择 x1:x2 之间，然后第二个维度选择所有，第三个维度选择组成的张量数据。总之在谈及张量的时候，即使是那些和空间关系很紧密的数据结构，我发现完全脱离几何思维，而只是单纯讨论维度会更方便些。

张量的dtype

numpy的 ndarray对象，有一个 dtype参数。表示目标张量数据结构所包含的数据类型。张量一般都包含的是数值型数据，也可能会有char型张量，但没有字符串型张量。不过我看到即使是单个字符，可能是处于字符编码问题考虑吧，但就算是纯英文的单个字符，我看到大家的通用做法还是建立字典，转成对应的数值型张量，估计计算速度也是一个考虑点吧。

样本维度

在深度学习领域，一般大家把第一个维度用作样本维度，所以我们看到MNIST例子中shape (60000,28,28)，第一个维度表示有60000个样本。

然后前面说到batch_size 是一次训练所含的样本数，所以实际一次训练模型送入的batch数据如下：

batch_size = 128
batch = train_images[:128] # 第一个批次
batch = train_iamges[128:256] # 第二个批次
...

利用tensorflow来实现一个单层神经网络

本文先用tensorflow来实现单层神经网络处理mnist问题，然后用keras来写一个两层神经网络来解决mnist问题。最后试着用keras编写一个简单的深度学习模型，也就是多层神经网络来解决mnist问题。

本文代码主要参考了keras的examples代码库，同时本文也考虑了一些输入数据的预处理统一化过程。

数据预处理

首先我们利用keras来下载mnist相关数据并进行必要的预处理操作。

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images.shape
(60000, 28, 28)
train_labels.shape
(60000,)

train_images 的shape第一维度是60000，说明有6万个图片，然后标签第一维度也是6万与之对应。

train_images = train_images.reshape((60000, 784))
train_images = train_images.astype('float32')
train_images = train_images / 255

第一步将第二维第三维数据合并到一维。

第二步是转换ndarray的dtype数据类型。

第三部是将数据0-255 归一化为 0- 1 。

类似的test_images也需要这样处理，这里就略过了。

标签数据需要进行one-hot编码处理：

from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
train_labels[0]
array([0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], dtype=float32)

one-hot编码的具体解释这里略过了，其他地方会讨论的。

感知器

感知器就是一层或者说单层神经网络。感知器类似于逻辑回归模型，只能做线性分类任务。

单层神经网络的编写用Keras非常的简单，但如果用tensorflow还是需要写一些代码的。不过作为一开始推荐还是用tensorflow来写一个简单的单层神经网络。因为Keras是基于tensorflow的更高层模块，这对于我们理解Keras具体做了什么工作很有帮助，也能帮助我们理解具体单层神经网络进行了那些数学运算。

x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
y_true = tf.placeholder(tf.float32, [None, 10])
y_logits = tf.matmul(x, W) + b
y_pred = tf.nn.softmax(y_logits )

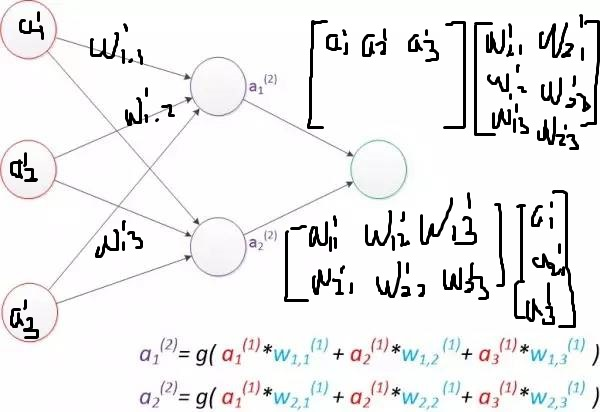
输入参数x第二维度784对应权重矩阵第一维度784，通常神经网络权重矩阵W的shape是(前一层节点数, 后一层节点数) 。这样输入参数矩阵x和权重矩阵W进行矩阵乘法【张量的点积，np.dot运算】之后得到第二维度等于权重矩阵第二维度的矩阵。输出的值数据送入 y_logits。这里 tf.matmul 就是进行的矩阵的乘法运算。

这里 tf.nn.softmax 是激活函数，具体softmax激活函数的讨论这里略过了。

交叉熵

tensorflow提供了专门的交叉熵计算函数，这里我们先用更原始的计算公式来看一下（参考了这篇文章）：

cross_entropy = -tf.reduce_sum(y_true * tf.log(y_pred))

大体过程如下所示：

$$ - \sum (1,0,0) * log((0.5,0.4,0.1)) = -(1log0.5 + 0log0.4 + 0*log0.1) = 0.301 $$

交叉熵越大那么预测值越偏离真实值，交叉熵越小那么预测值越接近真实值。

train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy) # 0.01是学习速率

使用tensorflow自带的交叉熵方法

推荐使用tensorflow自带的softmax+交叉熵方法来计算交叉熵，参考了这篇文章，说是计算会更稳定些。

现在让我们把到目前的代码整理一下：

import tensorflow as tf
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 784))
train_images = train_images.astype('float32')
train_images = train_images / 255
test_images = test_images.reshape((10000, 784))
test_images = test_images.astype('float32')
test_images = test_images / 255
from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
y_true = tf.placeholder(tf.float32, [None, 10])
y_logits = tf.matmul(x, W) + b
y_pred = tf.nn.softmax(y_logits )
cross_entropy = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits=y_logits , labels=y_true))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

好了，我们的例子进入收尾阶段了：

correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32)) 
with tf.Session() as sess:

    # Train
    sess.run(tf.global_variables_initializer())

    count = 0
    for _ in range(128):
        batch_xs = train_images[count*128:128*(count+1)]
        batch_ys = train_labels[count*128:128*(count+1)]
        sess.run(train_step, feed_dict={x: batch_xs, y_true: batch_ys})
        count += 1

        if count % 10 == 0:
            ans = sess.run(accuracy, feed_dict={x: test_images, y_true: test_labels})
            print("Accuracy: {:.4}%".format(ans*100))
    # LAST
    ans = sess.run(accuracy, feed_dict={x: test_images, y_true: test_labels})
    print("Accuracy: {:.4}%".format(ans*100))

关于tf.argmax 函数请看下面的例子。不感兴趣的可以略过，其作用就是把标签解释出来，不是这里的重点。

import tensorflow as tf
sess = tf.Session()
m = sess.run(tf.truncated_normal((5,10), stddev = 0.1) )

-----
array([[ 0.0919205 ,  0.06030607,  0.01196606,  0.03031359, -0.13546242,
        -0.12748787, -0.09680127,  0.12220833,  0.15264732,  0.05449662],
       [ 0.01277541, -0.00535311,  0.03589706,  0.01658093, -0.16726552,
        -0.06979545, -0.14876817, -0.03735523, -0.0439501 ,  0.15896702],
       [-0.05869294, -0.14986654, -0.17551927,  0.08360171, -0.00648978,
        -0.03274798, -0.05770732,  0.01505487,  0.13726853, -0.01670119],
       [-0.02666636, -0.05316785, -0.05433881, -0.02210794,  0.01175172,
        -0.0674843 , -0.06402522,  0.00812987, -0.17738222,  0.01375954],
       [-0.01734987,  0.01096244, -0.19889738,  0.08350741, -0.00222254,
         0.05094135,  0.06777989, -0.01986633, -0.1863249 , -0.04648132]],
      dtype=float32)
---

col_max = sess.run(tf.argmax(m, 0) )
----
array([0, 0, 1, 2, 3, 4, 4, 0, 0, 1], dtype=int64)
---
row_max = sess.run(tf.argmax(m, 1) ) 
---
array([8, 9, 8, 9, 3], dtype=int64)
---

所以 tf.argmax 第二个参数是1，那么返回一行数值最大的那个index索引值。 tf.argmax(y_pred, 1) 返回的那个索引值在本例中比较简单，就是实际预测的数字值。

tf.reduce_mean 将所有维度的元素相加然后求平均值

这个例子最后就是调用tensorflow的作业流程，启动运算数据流。然后评估一下对于测试数据现在精度如何了。这些不是这里的重点。就单层神经网络来说mnist例子很难超过90%的。

利用keras实现一个多层感知器

多层感知器实际上就是两层全连接神经网络。理论上两层神经网络可以无限逼近任意连续的函数了。下面用Keras来实现一个多层感知器。

首先我们试着把上面单层神经网络用Keras写一遍，下面是准备数据过程，后面都一样的。

准备数据

import tensorflow as tf
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 784))
train_images = train_images.astype('float32')
train_images = train_images / 255
test_images = test_images.reshape((10000, 784))
test_images = test_images.astype('float32')
test_images = test_images / 255
from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)

建模

from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(10, activation='softmax', input_shape=(784,)))
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=128)

Epoch 1/5
60000/60000 [==============================] - 1s 13us/step - loss: 0.6063 - acc: 0.8482
Epoch 2/5
60000/60000 [==============================] - 1s 12us/step - loss: 0.3316 - acc: 0.9083
Epoch 3/5
60000/60000 [==============================] - 1s 12us/step - loss: 0.3025 - acc: 0.9159
Epoch 4/5
60000/60000 [==============================] - 1s 11us/step - loss: 0.2889 - acc: 0.9194
Epoch 5/5
60000/60000 [==============================] - 1s 12us/step - loss: 0.2806 - acc: 0.9219

score = model.evaluate(test_images, test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

Test loss: 0.2757013351589441
Test accuracy: 0.9232

结果大概也是差不多的。因为这个例子多运行几次epoch，但单层神经网络再怎么优化也只能到92%了。

上面的建模过程稍微加一行，我们就构建了一个多层感知器。一般多层神经网络前面的激活函数选relu会更好一些。也就多加了一层，最后输出节点数为10的神经网络。

from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dense(10, activation='softmax'))
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=128)

Epoch 1/5
60000/60000 [==============================] - 5s 85us/step - loss: 0.2569 - acc: 0.9258
Epoch 2/5
60000/60000 [==============================] - 5s 84us/step - loss: 0.1037 - acc: 0.9688
Epoch 3/5
60000/60000 [==============================] - 5s 87us/step - loss: 0.0685 - acc: 0.9790
Epoch 4/5
60000/60000 [==============================] - 5s 85us/step - loss: 0.0508 - acc: 0.9848
Epoch 5/5
60000/60000 [==============================] - 5s 87us/step - loss: 0.0368 - acc: 0.9888

Test loss: 0.07560657636675751
Test accuracy: 0.9777

精度能够到97%了。

下面是Keras代码库examples里面的解决mnist问题的多层感知器，我根据上面的讨论将代码稍微调整下，建模过程如下：

from keras.models import Sequential
from keras.layers import Dense,Dropout
from keras.optimizers import RMSprop
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dense(512, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.summary()

区别就是又加了一层神经网络。

Epoch 1/5
60000/60000 [==============================] - 8s 139us/step - loss: 0.2197 - acc: 0.9320
Epoch 2/5
60000/60000 [==============================] - 8s 140us/step - loss: 0.0815 - acc: 0.9750
Epoch 3/5
60000/60000 [==============================] - 9s 145us/step - loss: 0.0530 - acc: 0.9836
Epoch 4/5
60000/60000 [==============================] - 9s 151us/step - loss: 0.0374 - acc: 0.9886
Epoch 5/5
60000/60000 [==============================] - 9s 151us/step - loss: 0.0302 - acc: 0.9899

Test loss: 0.08149926771794035
Test accuracy: 0.9808

examples里面还新加入了Dropout层，这个是一种过拟合技术，我们加上之后会如何：

from keras.models import Sequential
from keras.layers import Dense,Dropout
from keras.optimizers import RMSprop
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(10, activation='softmax'))
model.summary()

Epoch 1/5
60000/60000 [==============================] - 10s 162us/step - loss: 0.2439 - acc: 0.9253
Epoch 2/5
60000/60000 [==============================] - 10s 169us/step - loss: 0.1031 - acc: 0.9688
Epoch 3/5
60000/60000 [==============================] - 9s 151us/step - loss: 0.0760 - acc: 0.9771
Epoch 4/5
60000/60000 [==============================] - 10s 165us/step - loss: 0.0604 - acc: 0.9817
Epoch 5/5
60000/60000 [==============================] - 9s 155us/step - loss: 0.0512 - acc: 0.9846

Test loss: 0.07319687194137806
Test accuracy: 0.9814

区别其实不大，至少就mnist来说提升最大的是又新加入了一层神经网络，加入Dropout层没看出区别。

利用keras实现一个多层神经网络

卷积神经网络相关后面的讨论补上，这里我们主要来看下Keras代码库examples里面介绍的用CNN，深度学习神经网络来解决mnist问题效果如何。具体理解后面再说。

import tensorflow as tf
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

from keras import backend as K
if K.image_data_format() == 'channels_first':
    train_images = train_images.reshape(60000, 1, 28, 28)
    test_images = test_images.reshape(10000, 1, 28, 28)
    input_shape = (1, 28, 28)
else:
    train_images = train_images.reshape(60000, 28, 28, 1)
    test_images = test_images.reshape(10000, 28, 28, 1)
    input_shape = (28, 28, 1)

这里似乎涉及到不同backend的图形维度选择问题，这个后面再说。

train_images = train_images.astype('float32')
train_images = train_images / 255
test_images = test_images.astype('float32')
test_images = test_images / 255
from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)

继续之前的数据预处理。

from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import Adadelta
model = Sequential()
model.add(Conv2D(32, activation='relu', input_shape=input_shape, kernel_size=(3,3)))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
model.summary()

本例子跑起来开始有点慢了。Dropout应该不算一层，Flatten我估计不算一层，那么上面例子大概有5层。

Epoch 1/5
60000/60000 [==============================] - ETA: 0s - loss: 0.2683 - acc: 0.917 - 119s 2ms/step - loss: 0.2683 - acc: 0.9173
Epoch 2/5
60000/60000 [==============================] - 120s 2ms/step - loss: 0.0891 - acc: 0.9734
Epoch 3/5
60000/60000 [==============================] - 115s 2ms/step - loss: 0.0655 - acc: 0.9804
Epoch 4/5
60000/60000 [==============================] - 111s 2ms/step - loss: 0.0555 - acc: 0.9833
Epoch 5/5
60000/60000 [==============================] - 114s 2ms/step - loss: 0.0466 - acc: 0.9856

Test loss: 0.031076731445921907
Test accuracy: 0.9898

例子报道说epochs=12的时候精度能够上升到99%。

为了公平起见，绝对多层感知器和CNN神经网络这两个例子都按照epochs=12再跑一次来对比一下看看。

多层感知器：

Test loss: 0.08958661408673184
Test accuracy: 0.9821

和跑5次没有区别了。

CNN的看了一下个人PC CPU基本上跑满了，然后GPU没怎么用，tensorflow决定换成tensorflow-gpu 【PS：注意之前你用pip安装tensorflow了的，再安装个tensorflow-gpu即可，原来那个tensorflow包不能删的。】然后再看下。然后发现我这里显卡写着Intel UHD，似乎只有NAVID才能开启gpu，算了。

CNN神经网络：

Test loss: 0.028602463609369078
Test accuracy: 0.992

精度提升到了99%，看来CNN多训练几次后续效果还能提升，别小看了这1%的提升啊！

保存模型

一次训练有点费时了，那么如何保存训练好的模型呢？这个问题在keras文档FAQ里面有，算是很经典的一个问题了。

model.save('my_model.h5')

保存的数据有：

模型的结构，方便重新创造模型
模型训练得到的权重数据
训练损失和优化器配置
优化器状态，允许继续上一次训练

下次使用模型如下所示：

import tensorflow as tf
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

from keras import backend as K
if K.image_data_format() == 'channels_first':
    test_images = test_images.reshape(10000, 1, 28, 28)
    input_shape = (1, 28, 28)
else:
    test_images = test_images.reshape(10000, 28, 28, 1)
    input_shape = (28, 28, 1)


test_images = test_images.astype('float32')
test_images = test_images / 255
from keras.utils import to_categorical
test_labels = to_categorical(test_labels)

from keras.models import load_model
model = load_model('cnn_for_mnist_model.h5')

score = model.evaluate(test_images, test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])

Test loss: 0.028602463609369078
Test accuracy: 0.992

机器学习通用工作流程

定义问题，收集数据集

你的输入数据是什么？你要预测什么？
你面对的是什么类型的问题？是二分类问题还是多分类问题等等。

选择衡量成功的指标

模型要优化什么，它应该直接和你的业务目标相关。

确定评估方法

留出验证集数据量很大的时候采用具体操作就是训练数据里面一部分作为训练集，剩下来的一部分作为验证集，然后用训练集训练，验证集评估当前模型的好坏。模型参数调节好训练好之后，记得最后用整个训练集从头训练一次，最后用另外的测试集数据测试下模型的实际效果。
K折交叉验证
重复的K折验证

准备数据

数据张量化

神经网络的所有输入和输出目标都必须是浮点数张量（某些情况下可以是整数张量）。无论面对的是声音，文本，图像还是视频，都必须先将其转换成为张量。

数据标准化

之前我们看到的数据标准化情况有：

图像0-255数据整除缩减到 0-1 数据区间
如果是多个特征的数据，那么推荐如前面提及的进行z-score的标准化处理

mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

处理缺失值

对于神经网络来说，将缺失值设置为 0 是安全的。

特征工程

比如自然语言处理，根据自然语言处理学到的知识，选择二元模型对输入数据进行再处理。

良好的特征工程仍然可以让你用更少的资源更优雅地解决问题
良好的特征可以让你用更少的数据解决问题

开发比基准更好的模型

简单来说就是先随便开发一个小模型，要求不要太高，但至少要比随机乱猜准确率要高点的模型。

扩大模型规模，开发过拟合模型

一般是：

添加更多的层
让每一层变得更大
训练更多次数

要始终监控训练损失和验证损失，如果你发现模型随着训练次数增加在验证数据上性能下降了，那么就出现了过拟合。

模型正则化与调节超参数

这一步是最费时间的：你将不断调节模型，训练，验证，再调节模型... 。下面是一些你可能尝试的手段

添加Dropout层

Dropout层是深度学习之父Hinton和他的学生首次提出来的，它的原理很简单：对某一层使用dropout即该层在训练的时候会随机舍弃一些输出特征（也就是值变为0）。dropout比率是被设为0的特征所占的比例，一般设0.2~0.5之间。

添加Dropout层是最有效也最常用的正则化方法——正则化指降低过拟合。

尝试增加或者减少层

一般实践中开始会选择较少的层和节点数，然后逐渐增加之，直到这种增加对验证损失影响变得很小。

尝试L1 L2正则化

L1正则化和L2正则化都属于权重正则化，这是一种降低过拟合的方法，强制让模型权重只能取较小的值。

尝试不同的超参数

如每层的单元个数，优化器的学习率等。

附录

relu激活函数

relu激活函数具体的数学运算公式很简单，就是：

z = np.maximum(z, 0)

上面运算就是对z张量进行了relu运算了，按元素的，如果元素值大于0则为原元素的值，否则为0。

广播(broadcasting)

广播一种操作，shape较小的张量和shape较大的张量进行点对点运算时，需要对shape较小的张量进行广播操作，使其在运算上shape兼容。

广播具体操作规则是：

shape较小的张量添加新的维度是的两个张量维度数相同
shape较小的张量在新的维度中的数据是重复的，相当于没有原维度的数据，即： y[1,j] = y[2,j] = y[3,j] =... y[j]

张量点积

矩阵乘法也就是这里的张量点积学过线性代数的对这个概念还是很清楚了，不过到更高的维度的张量的点积情况似乎有点复杂了。这里我们需要把张量点积的shape变化弄清楚，后面可能会有用的，具体实际张量运算可以交给函数去做。

$$ x \cdot y = z $$

x shape (a, b) y shape (b,c) 输出 z的 shape(a, c)

高维的情况如下：

(a, b, c ,d) · (d,) -> (a,b,c)

(a, b, c ,d) · (d, e) -> (a,b,c, e)

张量变形

ndarray可以直接调用reshape方法来进行张量变形操作，变形后元素总个数应该不变，也就是各个维度容量乘积数不变。

张量的导数

张量的导数叫做梯度。

随机梯度下降(SGD)

小批量SGD过程如下：

抽取训练样本x和对应目标y组成数据批量
在x上运行网络，得到预测值y_pred
计算网络在这批数据上的损失，用于衡量y_pred和y之间的距离
计算损失相对于网络参数的梯度
将参数沿着梯度的反方向移动一点 W -= step * gradient ，从而使这批数据上的损失减小一点。这里的step即步长也叫学习率。

目前实践中的优化器optimizer都采用的是随机梯度下降，不同的是各自进行了某些优化，这些SGD变体有：带动量的SGD，Adagrad，RMSProp等。

均值移除

我更喜欢称之为z-score缩放，因为学习过统计学的就知道z-score标准分的含义，大体也知道这个缩放操作在做些什么事情。简单来说就是讲你的张量数据沿着各个特征维度，均值都为0，标准差都为1。

sklearn提供了 StandardScaler ，然后你利用它进行fit和tranform操作即可，你还可以继续利用之前的缩放器反向回滚 inverse_transform。

minmax缩放

就是控制你的张量数据的最小值和最大值范围。

sklearn提供了 MinMaxScaler 缩放器类，类似上面的你可以进行fit和tranform操作，同样可以利用之前的缩放器进行回滚操作。

归一化

sklearn提供了normalize函数来支持你的张量数据的归一化操作，这是一个不可逆的操作。具体就是让特征维度的数据绝对值之和为1。

二值化

就是给定一个阈值，你的张量数据转变成为0 1 值。这个估计在神经网络中有用。

onehot编码

onehot编码可以算是神经网络里面的基本入门知识了，简单来说就是将数值或者字符编码为空间扩展的 0 1 数值特征向量。具体sklearn提供了 OneHotEncoder 来进行相关操作。

比如说

[
    ['male', 10],
    ['female',5],
    ['male', 1]
]

其中性别特征列有值 male female 两个值这一列需要两个bit位。而后面的数字列有 1 5 10 三个值这个特征列需要三个bit位。上面的例子一共需要 5 个bit位。

df = pd.DataFrame( [
    ['male', 10],
    ['female',5],
    ['male', 1]
])
encoder = get_onehot_encoder()
encoder.fit(df)
encoder.transform([['female',10]]).toarray()
array([[1., 0., 0., 0., 1.]])

上面的例子中 1 0 表示 female 0 0 1 表示 10 。

label编码

label编码的含义也是很直接简单的，就是给定一个字典值，然后给这些字典里面的单词赋值0,2,3...这样你的张量数据就变成了数值型了。

具体sklearn提供了 LabelEncoder 来进行相关操作。

计算误差

平均绝对误差MAE

数据集所有数据点的绝对误差的平均值

import sklearn.metrics as sm
sm.mean_absolute_error(test_data, test_pred)

均方误差MSE

数据集所有数据点的误差的平方的平均值

sm.mean_squared_error(test_data, test_pred)

均方根误差RMSE

均方误差开个根号，为了更好地描述模型的误差

中位数绝对误差

数据集所有数据点的误差的中位数

sm.median_absolute_error(test_data, test_pred)

解释方差分

这个分数用来衡量我们的模型对于数据集波动的解释能力

sm.explained_variance_score(test_data, test_pred)

R方得分 R2 score

用来衡量模型对于未知样本的预测效果。

sm.r2_score(test_data, test_pred)

参考资料

机器学习实战 Peter Harrington 著李锐李鹏等译
机器学习实战线上教程
python深度学习弗朗索瓦·肖奈
deep learning 中文版
机器学习周志华著
这个文章介绍神经网络写的很好
这篇文章不错
python机器学习经典案例 Prateek Joshi 著陶俊杰陈小莉译