算法复杂度
一般讨论算法复杂度主要关注的是算法的时间复杂度,真到了该思考算法的时间复杂度了,那么这时算法将应对的是一个输入规模n很大的情况。人们提出大O表示法来描述一个算法在面对操作数n很大,或者输入数规模n很大的情况时,算法的计算时间和这个操作数n的关系。对于一个输入规模n很大的情况,还关心最开始某个变量的赋值啊,那个条件的判断啊,或者某个文件的加载那多出来的几步是没有意义的,因为随着操作数n的扩大,这些步骤如果和n无关,那么就是耗费的常数时间项,即使是这个时间有几秒,在后面的也会变得无足轻重起来。
若算法和输入规模n无关,则记为O(1) 常数运行时间。
然后我们经常看到这样的循环语句:
for i in range(n):
print(i)
这个循环和输入规模n相关,我们记作 O(n) 线性运行时间。
假设一个算法里面又有上面提到的O(1) ,又有上面的O(n) ,那么我们应该将O(1) 项去掉:
如果运行时间是一个多项式的和,那么保留增长速度最快的项,去掉其他各项
那么上面提到的算法复杂度就可简单记为 O(n) 。
又假设有个算法,有两个这样的循环:
for i in range(n):
print(i)
for i in range(n):
print(i)
按照道理讲其算法复杂度应该记作 2n ,大O表示法还有下面规则:
如果各个项是一个乘积,去掉所有的常数
也就是上面的算法复杂度是 O(2n) 最后简化为 O(n) ,这样整个算法仍然是线性运行时间。
如果是两个循环嵌套的情况:
for i in range(n):
for j in range(n):
print(i,j)
其具体运行了 n*n次,这个算法复杂度记为 $O(n^2)$ ,是二次多项式运行时间。此外可能会有其他情况,就是第二层循环会多运行几次或者少运行几次,这些都是细枝末节了,按照上面说的第一条规则:最后展开那些增长速度较慢的项将被去除,最后还是只剩下 $O(n^2)$ 。
递归的情况
以阶乘函数为例,递归函数的计算复杂度是递归函数最后展开为:
对数复杂度
在考量对数复杂度的时候是不关心对数的底数的,因为上面提及的第二条规则乘积的常数项可以忽略。
while n > 0:
print(1)
n = n//10
上面的例子读者看的出来这个循环次数大约为输入规模n的对数次,也就是 O(logn) 。
二分查找算法的计算复杂度也是对数复杂度,其大致以2为底数逐步压缩查找空间。
对数线性复杂度
O(nlog(n)) 快速排序算法的计算复杂度就是对数线性复杂度。
def quick_sort(seq):
"""
10000 的随机数列表排序:
select_sort use time 3.0919713973999023
quick sort use time 0.024930477142333984
:param seq:
:return:
"""
if len(seq) < 2:
return seq
else:
pivot = seq[0]
less_part = [i for i in seq[1:] if i <= pivot]
greater_part = [i for i in seq[1:] if i > pivot]
return quick_sort(less_part) + [pivot] + quick_sort(greater_part)
def selection_sort(seq):
"""
两种写法速度都差不多的,那么优先写的直白点的。
:param seq:
:return:
"""
def find_smallest_index(seq):
smallest = seq[0]
smallest_index = 0
for i in range(1, len(seq)):
target = seq[i]
if target < smallest:
smallest = target
smallest_index = i
return smallest_index
res = []
seq_copy = seq.copy()
for i in range(0, len(seq)):
smallest_index = find_smallest_index(seq_copy)
res.append(seq_copy.pop(smallest_index))
return res
选择排序计算复杂度粗略估计是长度的 $O(n^2)$ ,非常直观的算法里面有个循环套循环。
选择排序和快速排序可以说非常直观地说明了计算复杂度等级不同,运算效率的提升有多明显。我测试的结果是:
10000 的随机数列表排序:
select_sort use time 3.0919713973999023
quick sort use time 0.024930477142333984
是的,速度提升了接近100倍。
快速排序计算复杂度的估算里面有两部分:
-
小部分和大部分合计约n的比较判断操作
-
递归层级展开,递归层级深度展开要看你选的那个pivot分割点情况如何,最不好的情况这个pivot总是最小的,那么递归树深度带来的复杂度将达到O(n);最好的情况就是pivot分割点均分列表,于是递归树深度带来的复杂度是 $log_2n$ 。
实际情况既不是最好也不是最坏,考虑到对数复杂度是可以不考虑log函数的底数因子的,所以可以认为快速排序计算复杂度就是 $O(n\log(n))$ 。
python语言里面使用的排序算法
蒂姆·彼得斯因不满python以前的排序算法(估计应该是类似于快速排序的存在),于2002年发明了timsort算法,其基本思路应该也是类似于快速排序,不过利用了数据集数据已经部分有序的情况,进行了优化。
python里面的list.sort或者sorted函数就是使用的timsort算法。
字典
字典里面查找key计算复杂度是O(1),和字典长度无关,其内部使用的散列表算法。
我以前认为python的字典是基于红黑树或者二叉搜索树实现的,理解错了。python中的字典是基于hash table 散列表实现的,其查、插入、删除的计算复杂度都是 O(1) ,具体就是引入一个散列函数,将一个大规模输入空间映射到一个小的输出空间,将数量巨大的key转换成为数量较少的整数索引。
二分查找
二分查找以前也接触过吧,当时不怎么重视,认为就是一种快速查找方法了,参看 这个网页 ,其认为python的 index 方法并不是使用的二分查找,所以对大规模查询会很吃力。考虑到python一般的sequence对象都没有预排序,所以这种说法可信度还是很高的。然后利用python的 bisect 模块,我们可以构建出一种预排序的支持更快查询的接口,其内部就是使用的二分查找。
二分查找的基本思想就是对于一个已经排序了的列表,如果要查找某个元素的话,则将目标列表二分为两段,目标元素和分割点的元素进行大小比较,如果目标元素比分割点的元素小,则说明列表中那个要找的元素假设存在的话那么其应该在较小的那个区段,如果较大的话则在较大的那个区段,然后逐步这样递归来缩小查找区间,直到找到目标元素具体在列表的那个位置,或者发现不在列表中。
最近在看MIT的那个视频,其中第三课讲到了利用二分查找的思想来求解平方根的问题,这个对我启发很大。尤其是那一句: 任何计算机问题如果找不到好的方法,实际上都可以穷举而得,而穷举的过程,我们不需要一个个都试一下,我们只需要将这些可能的结果集排序之后,进行二分查找来快速缩小可能的结果集,那么我们就可以逐步更快地趋近理想结果了。
这使得我认识到,二分查找思想的应用可不限于查找,而是看作一种更普遍的计算思想。本文先试着从更抽象的角度来讨论二分查找。
抽象的二分查找思想讨论
现在我们将可能的结果集认为是某个函数f(x)的输入参数,然后我们有目标参数target,令f(x)=target的时候我们说我们就找到了目标结果x,或者说目标x符合函数f(x)=target这个关系。然后假设我们的考察对象f(x)在目标结果集内存在简单的增减关系,即目标集合可以由此排序,那么我们就可以开展二分查找来找到目标结果x了。
以相等查找为例,f(x)函数即f(x)=x,也就是输入什么同样输出的是什么。如果x=target,则我们说目标x符合条件f(x)=target,则该x就是我们要找的目标结果x。
如果我们定义 f(x)=x*x,则意思是我们要找某个x符合条件 x*x=target ,这就是求平方根的过程。
def binary_search_func(seq, target, func=lambda x: x, round_n=4, approx=True):
"""
use binary search to solve f(x) = target problem, if the function is a
monotonic function.
seq list or tuple
target found target in which case is the f(x) = target
func the monotonic function
round_n accurate to how many decimal point
approx the approx mode
if approx=True found target or some nearly target, return it's index
if approx=False found target index otherwise return -1
"""
low = 0
high = len(seq) - 1
count = 0
if approx:
target = round(target, round_n)
while low < high:
count += 1
mid = (high + low) // 2
guess = func(seq[mid])
if approx:
guess = round(guess, round_n)
if guess < target: # equal target the target also placed in big region.
low = mid + 1
else: # target in low region
high = mid
logger.info('binary_search_func run {0} times'.format(count))
if approx:
return low
else:
return low if (low != len(seq) and seq[low] == target) else -1
首先我们来看最简单的查找匹配操作:
def test_binary_search_func2():
seq = list('abcdefg')
pos = binary_search_func(seq, 'e', approx=False)
assert seq[pos] == 'e'
然后我们要求平方根,也就是某个 x*x=target 的过程,把之前定义的函数简单改一下即可:
def f(x):
return x*x
然后我们利用numpy的 arange 函数来生成一个可能结果集。
>>> import numpy as np
>>> np.arange(0,10,0.1)
array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ,
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1,
2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3,
4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2, 5.3, 5.4,
5.5, 5.6, 5.7, 5.8, 5.9, 6. , 6.1, 6.2, 6.3, 6.4, 6.5,
6.6, 6.7, 6.8, 6.9, 7. , 7.1, 7.2, 7.3, 7.4, 7.5, 7.6,
7.7, 7.8, 7.9, 8. , 8.1, 8.2, 8.3, 8.4, 8.5, 8.6, 8.7,
8.8, 8.9, 9. , 9.1, 9.2, 9.3, 9.4, 9.5, 9.6, 9.7, 9.8,
9.9])
>>>
然后我们有:
def test_binary_search_func():
import numpy as np
round_n = 6
seq = np.arange(0, 10, 10 ** (-round_n))
mid = binary_search_func(seq, 2, func=lambda x: x * x, round_n=6,
approx=True)
assert pytest.approx(seq[mid]) == 1.414214
bisect模块
bisect模块提供了二分查找的支持,比如bisect_left函数:
def bisect_left(a, x, lo=0, hi=None):
"""Return the index where to insert item x in list a, assuming a is sorted.
The return value i is such that all e in a[:i] have e < x, and all e in
a[i:] have e >= x. So if x already appears in the list, a.insert(x) will
insert just before the leftmost x already there.
Optional args lo (default 0) and hi (default len(a)) bound the
slice of a to be searched.
"""
if lo < 0:
raise ValueError('lo must be non-negative')
if hi is None:
hi = len(a)
while lo < hi:
mid = (lo+hi)//2
if a[mid] < x: lo = mid+1
else: hi = mid
return lo
其底层有c加速,然后其返回的是一个索引值,根据这个索引值,如果你执行 a.insert(x) ,那么将把目标值插入到目标位置,如果x已经在a中存在,则插入的是最左边的位置。于是我们有:
def binary_search(seq, target):
"""
use the bisect_left.
"""
pos = bisect_left(seq, target)
# pos == len(seq) means the target is bigger than all the elements of seq
# other pos value is a valid index in seq
# So if x already appears in the list, a.insert(x) will
# insert just before the leftmost x already there.
return pos if (pos != len(seq) and seq[pos] == target) else -1
iter_search
在这里讲个题外话,提到可能结果集的时候,我就想到将多个函数参数作为(a,b,c)这种形式,可是这种多元函数问题,怎么排序,怎么比较大小,怎么确定增减性?所以只好回滚到最原始的穷举过程。
比如说孙子算经里面的:
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
穷举的基本函数是:
def iter_search(f,seq,target):
for item in seq:
if f(item) == target:
yield item
很简单的一个函数,很简单的逻辑,但实际上这种先迭代某个对象,然后找到某个对象复合某个条件,则返回某个对象的过程在程序模式里面是非常常见的。
然后我们根据笛卡尔积生成可能结果集:
>>> from itertools import product
>>> seq = list(product(range(35),range(35)))
>>> seq
[(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), ..............
.............
然后我们可以很直观的将问题化为两个满足条件来对可能结果集进行过滤操作:
def f(d):
x = d[0]
y = d[1]
head = x + y
return head
def g(d):
x = d[0]
y = d[1]
foot = 2*x + 4*y
return foot
然后我们有:
res = list(product(range(35),range(35)))
res = iter_search(f,res,35)
res = iter_search(g,res,94)
print(list(res))
[(23, 12)]
选择排序
选择排序基本思路是非常直观的,就是遍历序列,找到最小的那个,将其放在第一位,然后剩下的继续找最小的。作为排序算法的第二梯队,第一梯队是指快速排序和其他变种,冒泡排序显得有点故弄玄虚了。对于不是特别的大型序列来说,实际上选择排序仍然是不错的算法。
下面先给出python语言版本的最易懂的写法,和后面那种写法从算法运行效率方面差别不大。
def select_sort2(seq):
"""
:param seq:
:return:
"""
def find_smallest_index(seq):
smallest = seq[0]
smallest_index = 0
for i in range(1, len(seq)):
target = seq[i]
if target < smallest:
smallest = target
smallest_index = i
return smallest_index
res = []
seq_copy = seq.copy()
for i in range(0, len(seq)):
smallest_index = find_smallest_index(seq_copy)
res.append(seq_copy.pop(smallest_index))
return res
上面这个实现之所以易懂是因为其就是选择排序思路的直接书写,找到最小的那个元素,然后取出,再找再取出,如此找完。
C语言版本
void select_sort(int array[], int num) {
int temp;
for (int i = 0; i < num; i++) {
for (int j = i + 1; j < num; j++) {
if (array[i] > array[j]) {
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
}
}
python语言版本
def select_sort(seq):
seq2 = seq.copy()
for i in range(0, len(seq2)):
minimum = i
for j in range(i + 1, len(seq2)):
if seq2[j] < seq2[minimum]:
minimum = j
seq2[i], seq2[minimum] = seq2[minimum], seq2[i]
return seq2
基本过程都大同小异,就是利用两个遍历动作来形成A,B这样的比较对,然后再决定采取什么行为。python语言版本一些额外的动作是因为希望返回的序列是另外的序列,原序列必变,而C语言版本原数组是就地修改的。
算法复杂度
选择排序计算复杂度粗略估计是长度的 $O(n^2)$ ,核心占用时间动作就是那个循环套循环。
这里就顺便说下快速排序,同样的python语言版本,10000个随机数列表排序用时如下:
10000 的随机数列表排序:
select_sort use time 3.0919713973999023
quick sort use time 0.024930477142333984
我们看到快速排序相比选择排序确实快了太多了。
快速排序
快速排序的基本思路是利用递归的思想,将大问题转变成小问题。
利用递归解决问题大概需要确定这两点:
- 递归的终点
- 递归问题的切分
快排递归的终点是如果序列长度小于2,则其顺序自然是有效的。
快排递归问题的切分是取一个点,这个点其实是随意的,将比这个元素小的放一边,将比这个元素大的放一边。于是形成了这样的有效顺序: less_part pivot greater_part 。然后对less_part 和 greater_part同样继续这样的操作,再将结果列表组合起来即可。
def quick_sort(seq):
"""
10000 random number seq :
select_sort use time 3.0919713973999023
quick sort use time 0.024930477142333984
"""
if len(seq) < 2:
return seq
else:
pivot = seq[0]
less_part = [i for i in seq[1:] if i <= pivot]
greater_part = [i for i in seq[1:] if i > pivot]
return quick_sort(less_part) + [pivot] + quick_sort(greater_part)
快排的算法复杂度是 O(nlogn),在排序算法里面算是第一梯队了,效率很高。当n不大的时候快速排序或者选择排序差别不大,当n很大的时候快速排序就比选择排序快很多了,具体奥秘就在其算法复杂度上。
快速排序计算复杂度的估算里面有两部分:
-
小部分和大部分合计约n的比较判断操作
-
递归层级展开,递归层级深度展开要看你选的那个pivot分割点情况如何,最不好的情况这个pivot总是最小的,那么递归树深度带来的复杂度将达到O(n);最好的情况就是pivot分割点均分列表,于是递归树深度带来的复杂度是 $log_2n$ 。
实际情况既不是最好也不是最坏,考虑到对数复杂度是可以不考虑log函数的底数因子的,所以可以认为快速排序计算复杂度就是 $O(n\log(n))$ 。
树建模
树应该也算作图的一种,不过具体到计算机算法数据结构这块树和图是分开讨论了。树和一般图的区别在于其有一个特殊的节点,该节点没有父节点被称作为根节点,也就是树的根节点入度为0,其他节点入度为1。节点的出度并没有限制。然后树是无环的。
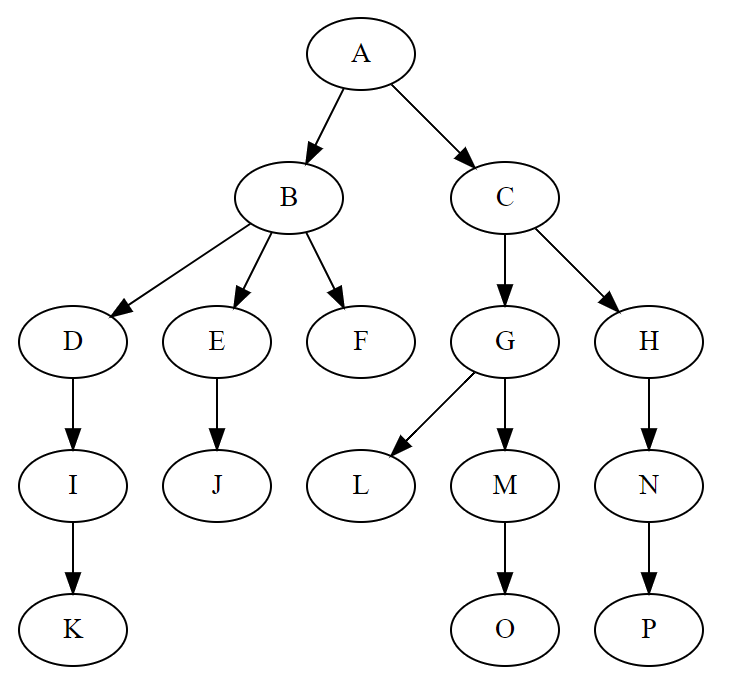
树被称为Tree,这些节点仍然称作 Node。取消树的入度称呼,用某节点的度degree来描述该节点的出度。新增parent和children概念,其中parent=None的节点为根节点,children为空的列表的表示该节点没有子节点,即度为0的终端节点。
从根节点开始定义根节点的层次level为1,下面根节点的子节点层次level为2,后面以此类推。
基本实现
class Tree(object):
"""
the brother nodes can not have the same name.
"""
def __init__(self, name, parent=None):
self.name = name
self.parent = parent
self.children = []
def __iter__(self):
"""
iter all nodes, dfs style.
"""
if self.name is not None:
yield self
for child in self.children:
for i in child:
yield i
def __str__(self):
if self.parent is None:
return '<Tree: {0}>'.format(self.name)
else:
return '<TreeNode: {0}>'.format(self.name)
def __repr__(self):
if self.parent is None:
return '<Tree: {0}>'.format(self.name)
else:
return '<TreeNode: {0}>'.format(self.name)
def has_node(self, node):
"""
check whether this tree has this node.
only check the node's name.
"""
if isinstance(node, Tree):
name = node.name
elif isinstance(node, str):
name = node
else:
raise TypeError("node wrong type")
for target in self:
if target.name == name:
return True
return False
def has_child(self, node):
"""
check whether this node has this child node.
only check the node's name
"""
if isinstance(node, Tree):
name = node.name
elif isinstance(node, str):
name = node
else:
raise TypeError("node wrong type")
for child in self.children:
if child.name == name:
return True
return False
def insert_child(self, parent_name, child_name):
"""
insert a child
"""
target = self[parent_name]
if target.has_child(child_name):
raise Exception("child name exists")
else:
target.children.append(Tree(child_name, parent=target))
def __getitem__(self, name):
"""
get target node only return first found one
"""
for target in self:
if target.name == name:
return target
raise KeyError
def get_nodes(self, name):
"""
get all target
"""
for target in self:
if target.name == name:
yield target
def to_json(self):
return {self.name: [i.to_json() for i in self.children]}
@property
def level(self):
level = 1
target = self
while target.parent is not None:
level += 1
target = target.parent
return level
二叉搜索树
二叉搜索树(Binary Search Tree):
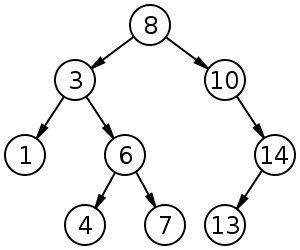
其每一个节点都至多有两个子节点,然后所有的节点都满足以下三个条件
- 左节点的值小于它的父节点
- 右节点的值大于它的父节点
- 所有节点的值均不相等
二叉搜索树的插入复杂度是 O(log n) ,查找复杂度最好情况 O(log n) ,最坏情况 O(n) 。
比如上面图片的那个二叉树,假设我们要插入19,那么首先和8比较,大,则右,再和10比较,大则右,再和14比较,大则右,然后空就可以插入了。
然后假设我们要查找19,那么过程大体也是类似的和8比较,大则右,再和10比较,大则右,再和14比较,大则右,然后相等则找到。
基本实现
我们在 树算法建模初步 中构建的Tree类继续来实现 BinarySearchTree 类。首先我们定义目标节点的左节点left和右节点right,一个是children的第一个元素,一个是children的第二个元素。
@property
def left(self):
if len(self.children) == 0:
self.children = [None, None]
elif len(self.children) == 1:
self.children.append(None)
return self.children[0]
@left.setter
def left(self, node):
self.children[0] = node
@property
def right(self):
if len(self.children) == 0:
self.children = [None, None]
elif len(self.children) == 1:
self.children.append(None)
return self.children[1]
@right.setter
def right(self, node):
self.children[-1] = node
插入动作
按照二叉搜索树的定义,我们需要编写插入动作和查找动作。普通的树要插入某个节点是需要指明在那个父节点插入的,而二叉搜索树是说我要插入什么节点就直接往整个树上插入的,具体位置会自动计算得到的。此外二叉搜索树插入动作和查找动作依赖于一个比较大小的过程,树的节点的name是随意的字符串,并不是很好比较大小。
下面比较大小将会采用python的hash函数。通过 hash(object) 也就是调用object的 __hash__ 方法。值得一提的是这里的比较大小,并不具有某种实际意义,比如:
>>> hash(11)> hash("22")
True
def insert(self, name):
if hash(name) < hash(self.name):
if self.left is None:
self.left = BinarySearchTree(name, parent=self)
else:
self.left.insert(name)
elif hash(name) > hash(self.name):
if self.right is None:
self.right = BinarySearchTree(name, parent=self)
else:
self.right.insert(name)
else:
self.name = name
插入动作的代码过程非常清晰,几乎和上面描述的二叉搜索树的定义过程类似。小的往左边插,大的往右边插。
查找动作
查找动作也类似上面插入动作的描述:
def find(self, name):
if hash(name) < hash(self.name):
if self.left is None:
return False
else:
return self.left.find(name)
elif hash(name) > hash(self.name):
if self.right is None:
return False
else:
return self.right.find(name)
else:
return self
图建模
我们在解决现实世界中的一些问题的时候,常常很自然地进行一些作图来试着对这些问题进行建模,其中有一些问题的最核心的部分可以精简为如下一种用小圆点和连接这些小圆点的直线来表示出来:
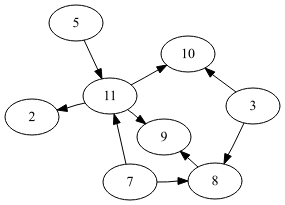
这些小圆点叫做 顶点 ,连接这些顶点的直线或者曲线叫做 边 。
顶点记作Node,边记作edge。然后整个图的所有顶点数目叫做该图的阶,记作Order。
图里面的边可能有方向也可能没方向,一般用带箭头的直线来表示该边有方向。如果边没有方向,那么叫做 无向图,如果线有方向,那么叫做 有向图 。
在有向图里面,有 入度 和 出度 这两个专业术语,其中某个顶点的入度是指进入该顶点的边条数;而某个顶点的出度是指从该顶点出来的边条数。其中入度记作 in-degree , 出度记作 out-degree。
Graph类
class Graph(ABC):
"""
general graph class
"""
DIRECTED = None
@abstractmethod
def nodes(self):
raise NotImplementedError("Not Implement nodes methods")
@abstractmethod
def neighbors(self, node):
raise NotImplementedError("Not Implement neighbors methods")
@abstractmethod
def edges(self):
raise NotImplementedError("Not Implement edges methods")
@abstractmethod
def has_node(self, node):
raise NotImplementedError("Not Implement has_node methods")
@abstractmethod
def has_edge(self, edge):
raise NotImplementedError("Not Implement has_edge methods")
@abstractmethod
def add_node(self, node):
raise NotImplementedError("Not Implement add_node methods")
@abstractmethod
def add_edge(self, edge):
raise NotImplementedError("Not Implement add_edge methods")
图Graph是抽象基类,具体后面某个图要么是有向图要么是无向图,这个后面再讨论。
这里定义了一些基本的方法,要求后面的图具体实现都应该有这些方法:
- DIRECTED 属性: True说明该图是有向图,False则说明该图是无向图。
- nodes方法:遍历本图的各个顶点
- neighbors方法:返回与某个顶点相邻的顶点
- edges方法:遍历本图的各个边,这个也是一个抽象方法,这样具体边的相似判断可以往后面放。
- has_node方法:本图是否有该顶点,这里顶点是某个唯一标识的字符串
- has_edge方法:本图是否有该边,同样具体edge的存储形式和判断都往后面放。
- add_node方法:增加一个节点
- add_edge方法: 增加一个边
UndirectedGraph类
无向图的数据采用这样的形式:
{
'a': {'b','z'}
}
该字典的keys表示该图的所有顶点,然后后面的值就是具体与该顶点相邻的那些顶点,于是有:
class UndirectedGraph(Graph):
"""
graph_data structure as:
{
'a': {'b','z'}
}
"""
DIRECTED = False
def __init__(self, graph_data=None):
"""
Initialize a graph.
"""
if graph_data is None:
self.graph_data = {}
else:
self.graph_data = graph_data
def nodes(self):
"""
Return node list.
"""
return self.graph_data.keys()
def neighbors(self, node) -> list:
"""
Return all nodes that are directly accessible from given node.
"""
return list(self.graph_data[node])
接下来遍历边一个技巧是使用字典 {a,b} 这样的形式来表示无向图的边,这样边就和连接的两个顶点的顺序无关了。
NOTICE 顶点a到顶点a的边字典形式是 {a} ,其长度为1,这需要额外处理一下。
def _read_edge(self, edge):
data = copy(edge)
if len(data) == 1:
u = v = data.pop()
elif len(data) == 2:
u, v = data
else:
raise Exception("wrong edge format")
return u, v
def _generate_edges(self):
"""
represent edge as {a,b}
"""
edges = []
for node in self.nodes():
for neighbour in self.neighbors(node):
if {neighbour, node} not in edges:
edges.append({node, neighbour})
return edges
def edges(self):
"""
Return all edges in the graph.
"""
return self._generate_edges()
def has_node(self, node) -> bool:
"""
Return whether the requested node exists.
"""
return node in self.graph_data
def has_edge(self, edge) -> bool:
"""
Return whether an edge exists.
"""
u, v = self._read_edge(edge)
return {u, v} in self.edges()
新增一个顶点和新增一个边后面再讨论,下面来看有向图那边的情况。
DirectedGraph类
有向图的数据存储结构为:
{
'a': ['b','z']
}
其中该字典的keys是该图的各个顶点,然后后面的值就是具体该顶点指向的那些相邻的顶点。于是有:
class DirectedGraph(Graph):
"""
graph_data structure as:
{
'a': ['b','z']
}
"""
DIRECTED = True
def __init__(self, graph_data=None):
"""
Initialize a graph.
"""
if graph_data is None:
self.graph_data = {}
else:
self.graph_data = graph_data
def nodes(self):
"""
Return nodes
"""
return self.graph_data.keys()
def neighbors(self, node):
"""
Return all nodes that are incident to the given node.
"""
return self.graph_data[node]
接下来是遍历边的实现,其才用了 (a,b) 这样的形式来表示有向图的边,这样边就和连接的两个顶点的顺序有关了。
def _generate_edges(self):
"""
represent edge as (a,b)
"""
edges = []
for node in self.nodes():
for neighbor in self.neighbors(node):
if (node, neighbor) not in edges:
edges.append((node, neighbor))
return edges
def edges(self):
"""
Return all edges in the graph.
"""
return self._generate_edges()
def has_node(self, node) -> bool:
"""
Return whether the requested node exists.
"""
return node in self.graph_data
def has_edge(self, edge) -> bool:
"""
Return whether an edge exists.
"""
u, v = edge
return (u, v) in self.edges()
增加节点
无向图是:
def add_node(self, node):
"""
Add given node to the graph.
"""
if self.has_node(node):
raise AdditionError("Node %s already in graph" % node)
self.graph_data[node] = set()
有向图是:
def add_node(self, node):
"""
Add given node to the graph.
"""
if self.has_node(node):
raise AdditionError("Node {0} already in digraph".format(node))
self.graph_data[node] = []
这个没啥好说的。
增加边
无向图:
def add_edge(self, edge):
"""
Add an edge to the graph connecting two nodes.
"""
u, v = self._read_edge(edge)
if self.has_edge(edge):
raise AdditionError("Edge ({0}, {1}) already in graph".format(u, v))
for n in [u, v]:
if n not in self.graph_data:
self.add_node(n)
self.graph_data[u].add(v)
if u != v:
self.graph_data[v].add(u)
有向图:
def add_edge(self, edge):
"""
Add an directed edge to the graph connecting two nodes.
"""
u, v = edge
if self.has_edge(edge):
raise AdditionError("Edge (%s, %s) already in digraph" % (u, v))
for n in [u, v]:
if n not in self.graph_data:
self.add_node(n)
self.graph_data[u].append(v)
这里我们利用之前已经写好的 has_edge 方法会让程序逻辑更清晰一些。
无向图因为没有方向,所有从u到v和从v到u需要添加两次。
有向图的入度和出度
def out_degree(self, node):
"""
return the target node's out degree
"""
count = 0
if node in self.graph_data:
count = len(self.graph_data[node])
return count
def in_degree(self, node):
"""
return the target node's in degree
"""
count = 0
for k, v in self.graph_data.items():
if node in v:
count += 1
return count
广度优先搜索和深度优先搜索
广度优先搜索,英文名:breadth-first-search,可简写为bfs。深度优先搜索,英文名:depth-first-search,可简写为dfs。
广度优先搜索和深度优先搜索应用范围很广,既可用于图数据结构,也可用于树数据结构。其首先是一种遍历图或者树的搜索方法,其次就是利用这种遍历的过程来解决一些问题,比如求解两个节点之间的最短路径问题。
广度优先搜索在搜索过程中一般是利用一个队列来存储待处理的节点,然后在图的搜索上,是每往外扩展一级就将这些子节点加入到待处理的任务中去。
深度优先搜索是利用一种递归的写法,函数一直深入查找子节点,直到找不到子节点为止;然后再返回之前未做完的节点任务继续处理。
广度优先搜索
def bfs_search(self, start):
"""
Breadth-first search.
"""
def bfs():
"""
Breadth-first search sub-function.
"""
while queue:
node = queue.popleft()
if node not in visited:
for other in self.neighbors(node):
bfs_tree.insert_child(node, other)
queue.append(other)
visited.append(node)
queue = deque() # Visiting queue
visited = []
bfs_tree = Tree(start)
queue.append(start)
bfs()
return bfs_tree
这里我们利用在 树算法建模初步 中讨论的Tree类树数据结构来进行遍历过程生成树的结果存储。
深度优先搜索
def dfs_search(self, start):
"""
Depth-first search.
"""
def dfs(node):
"""
Depth-first search sub-function.
"""
for other in self.neighbors(node):
dfs_tree.insert_child(node, other)
dfs(other)
dfs_tree = Tree(start)
dfs(start)
return dfs_tree
最小路径问题求解
当我们求出了那个生成树,实际上最小路径问题,从start到end,选择end那个level层级最小的节点,然后最小路径就出来了。这其中可以对上面的生成树过程做一些小的优化:
def bfs_shortest_path_search(self, start, end):
def bfs():
"""
Breadth-first search sub-function.
"""
while queue:
node = queue.popleft()
if node not in visited:
for other in self.neighbors(node):
if other == end:
bfs_tree.insert_child(node, other)
break
else:
bfs_tree.insert_child(node, other)
queue.append(other)
visited.append(node)
queue = deque() # Visiting queue
visited = []
bfs_tree = Tree(start)
queue.append(start)
bfs()
return bfs_tree
def dfs_shortest_path_search(self, start, end):
def dfs(node):
"""
Depth-first search sub-function.
"""
for other in self.neighbors(node):
if other == end:
dfs_tree.insert_child(node, other)
break
else:
dfs_tree.insert_child(node, other)
dfs(other)
dfs_tree = Tree(start)
dfs(start)
return dfs_tree
具体就是当找到目标节点之后,至少我们能够确认目标节点的兄弟节点是没必要再找下去了,因为再找下去只可能是更长的路径。
有向无环图
有向无环图 ,英文缩写是 DAG,(directied acyclic graph)。其是在有向图的基础上加入了无环这个判断条件。所谓无环指在该有向图从任意顶点出发经过若干条边之后都无法回到该顶点。
一开始我最先接触 DAG 这个术语,是在找工作流软件的时候,工作流的通用表示方法就是用 DAG 来表示。为什么?假设你是工作流中的某个节点的员工,你按照某个workflow走下去,最后闭环了,然后你无限循环在某个流程中了,那可真蠢了。
然后比如说 git 的版本控制,其内部版本控制流程也是用的有向无环图,如果你版本修改修改,又回到某个老版本了,那版本控制也失效了。
聪明的朋友肯定想到了我们的宇宙时间是不可逆的,也就是说如果用模型来表示宇宙所有的信息数据变动流结构的话,那么一定是有向无环图。
在之前的 图算法建模初步 中我们已经实现了有向图 DirectedGraph 类,在该类的基础上只需要加上额外的无环判断操作即可。
图论里面关于这个已经有算法了,我们也没什么好想的,就是图论的拓扑排序方法来判断一个有向图是否是无环的。
wiki上有伪代码,我们可以下看一下:
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
这个算法叫做 Kahn 算法,具体思路就是请读者假想目标研究有向图里面有一个闭环,那么这个闭环里面的所有节点都有进入箭头的,也就是其不可能在set S,其在算法中只可能在 m 中被选中,而且闭环中的节点一定不会出现在n中,这样上面的算法再怎么运算,if语句对于闭环中的m来说都不会成立。
然后假设某几个节点都有入口,那么顺藤摸瓜,逐个删除是可以把这些节点都放到S里面去的。
我心里还有一个担心,也就是上面的算法的终止问题,主要是闭环那边。初步的判断是闭环内的节点m不会进入S,其他节点慢慢会被放入L。OK,让我们开始写代码,然后再实际看一下吧。
基本实现
该类继承自有向图类,然后修改增加边的动作,加上sort无环判断,如果发现增加一个边之后图有环了,那么将移除该边,并抛出异常。
就sort方法的实现来说基本上就是上面提及的wiki的伪代码的实际实现:
class DirectedAcyclicGraph(DirectedGraph):
def add_edge(self, edge):
"""
add acyclic judgement.
"""
super().add_edge(edge)
if not self.sort():
self.remove_edge(edge)
raise NotAcyclicError
def remove_edge(self, edge):
"""
remove edge start -> end
"""
start, end = edge
super(DirectedAcyclicGraph, self).del_edge((start, end))
# clear data
if self.in_degree(start) == 0 and self.out_degree(start) == 0:
if start in self.graph_data:
del self.graph_data[start]
if self.in_degree(end) == 0 and self.out_degree(end) == 0:
if end in self.graph_data:
del self.graph_data[end]
def sort(self):
"""
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
"""
target = deepcopy(self)
top_order = []
queue = deque()
for k in target.nodes():
if target.in_degree(k) == 0:
queue.append(k)
logger.debug('queue append {0}'.format(k))
while queue:
n = queue.pop()
top_order.append(n)
for m in self.neighbors(n):
target.remove_edge((n, m))
logger.debug('remove n->m {0} {1}'.format(n, m))
if target.in_degree(m) == 0:
logger.debug('append {0}'.format(m))
queue.append(m)
if len(top_order) != len(self.nodes()):
return False
else:
return top_order
任何问题总可以通过暴力穷举算法求解,当然有些问题组合数情况太多了,尤其是某些问题,没有快速算法,即NP完全问题。那么可以试着用一些近似算法来快速找到一个近似解。贪婪算法就是其中的一个近似解。
贪婪算法并不是某种具体的算法,更像是写算法时的一种思路参考。如果你要解决问题,而该问题可以分解为多个步骤,那么你可以通过寻找每步的局部最优解,来近似得到目标问题的全局最优解。(贪婪算法并不保证你得到的解一定是全局最优解,但一般这个解是很靠近全局最优解了。)
对于一个问题,如果贪婪算法是有效的,那么一般贪婪算法就是解决这个问题最好的算法。
背包问题
class Knapsack(object):
def __init__(self, capacity, items=None):
self.capacity = capacity
self.items = [] if items is None else items
self.freespace = self.capacity
def add_item(self, item):
if self.freespace - item.weight >= 0:
self.freespace -= item.weight
self.items.append(item)
return True
else:
return False
def all_items_value(self):
value = 0
for item in self.items:
value += item.value
return value
def __repr__(self):
return '<Knapsack: {0}>'.format(self.items)
class Item(object):
def __init__(self, name, value, weight):
self.value = value
self.weight = weight
self.name = name
def __repr__(self):
return '<Item: {0}>'.format(self.name)
def __eq__(self, other):
if self.name == other.name and self.value == other.value and self.weight == other.weight:
return True
else:
return False
def greedy_algorithm(knapsack, items):
"""
贪婪法求解
:return:
"""
items_copy = items.copy()
found = True
while found:
max_value = 0
choosed_item = None
for item in items_copy:
if item.value > max_value:
choosed_item = item
max_value = choosed_item.value
if knapsack.add_item(choosed_item):
found = True
items_copy.remove(choosed_item)
else:
found = False
return knapsack
上面的版本还可以扩展出比较函数是比较最小重量或者最大价值/重量比,总的说来这里理解贪婪算法基本思想即可。
蒙特卡罗模拟
蒙特卡罗模拟的蒙特卡罗是一个赌运气游戏的名字,而蒙特卡罗模拟在现代计算机发展到今天的背景下,这种思想已经越来越重要了。简单来说其试图将一个问题转成某种随机过程,然后用计算机来模拟这个随机过程从而得到解答。因为自然界存在着大量的问题,其本身就暗含随机性的,对于这样的过程对应建立基于随机性的模型是很直观的。不过还存在着一些问题,比如计算 $\pi$ 值,和随机性不是很相关的,但通过某个随机过程,也能计算出 $\pi$ 值。这种通过某个随机过程来试着解决某个问题的方法叫做蒙特卡罗方法。
下面是一个模拟随意游走的代码,参考了MIT的python编程导论一书:
import random
from math import sqrt
class Location(object):
def __init__(self, x, y):
self.x = x
self.y = y
def move(self, dx, dy):
return Location(self.x + dx, self.y + dy)
def get_x(self):
return self.x
def get_y(self):
return self.y
def distance(self, other):
ox, oy = other.x, other.y
distance = sqrt((self.x - ox) ** 2 + (self.y - oy) ** 2)
return distance
def __str__(self):
return f'<Location ({self.x}, {self.y})>'
class Drunk(object):
def __init__(self, name=None):
self.name = name
def __str__(self):
if self.name is not None:
return self.name
else:
return 'Anonymous'
class UsualDrunk(Drunk):
def take_step(self):
step_choices = [(0, 1), (0, -1), (1, 0), (-1, 0)]
return random.choice(step_choices)
class Field(object):
def __init__(self):
self.drunks = {}
def add_drunk(self, drunk, loc):
if isinstance(loc, (tuple, list)):
assert len(loc) == 2
loc = Location(loc[0], loc[1])
if drunk in self.drunks:
raise ValueError('Duplicate drunk')
else:
self.drunks[drunk] = loc
def move_drunk(self, drunk):
if drunk not in self.drunks:
raise ValueError('Drunk not in field')
dx, dy = drunk.take_step()
current_loc = self.drunks[drunk]
self.drunks[drunk] = current_loc.move(dx, dy)
def get_loc(self, drunk):
if drunk not in self.drunks:
raise ValueError('Drunk not in field')
return self.drunks[drunk]
def walk(f, d, num_steps):
start = f.get_loc(d)
for s in range(num_steps):
f.move_drunk(d)
return start.distance(f.get_loc(d))
def bulk_walk(num_steps, num_bulk, dClass):
"""
:param num_steps: 随机行走了多少步
:param num_bulk: 一批次进行了多少次实验
:param dClass: 醉汉类型
:return: distances 一批次里面每次开图的总共行走距离列表
"""
drunk = dClass()
origin = Location(0, 0)
distances = []
for i in range(num_bulk):
f = Field()
f.add_drunk(drunk, origin)
distances.append(round(walk(f, drunk, num_steps), 1))
return distances
def drunk_test(num_steps_batch, num_bulk, dClass):
"""
:param num_steps_batch: 随机行走多少步填入批次
:param num_bulk: 一批次进行了多少次实验
:param dClass: 醉汉类型
:return:
"""
mean_distance_list = []
for num_steps in num_steps_batch:
distances = bulk_walk(num_steps, num_bulk, dClass)
print(f'{dClass.__name__} random walk of {num_steps} steps')
mean_distance = round(sum(distances) / len(distances), 4)
mean_distance_list.append(mean_distance)
print(f'Mean = {mean_distance}')
print(f'Max = {max(distances)} Min = {min(distances)}')
return mean_distance_list
if __name__ == '__main__':
num_steps_batch = list(range(100, 3000, 100))
data = drunk_test(num_steps_batch, 100, UsualDrunk)
就作为代码都是很简单直观的一些代码。然后我们定义了如下 绘图函数:
def polyfit_plot(ax, x, y, deg=1, xlabel='', ylabel='', title='', **kwargs):
"""
多项式拟合绘图
:return:
"""
if xlabel:
ax.set_xlabel(xlabel)
if ylabel:
ax.set_ylabel(ylabel)
if title:
ax.set_title(title)
predict_func = np.poly1d(np.polyfit(x, y, deg))
out = ax.plot(x, y, '.', x, predict_func(x), '-', **kwargs)
return out
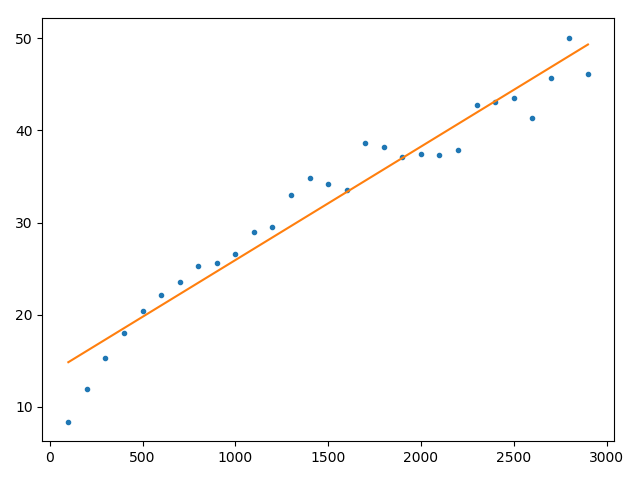
上面绘制这个简单的线性拟合线的时候,我想到了很多东西,现在热门的机器学习,和随机过程模拟,统计过程分析,基本作图演示等概念都是密不可分的。
比如说上面简单的一元函数拟合,在numpy提供的polyfit函数里面,本身就支持多次的,也就是直接就可以做多项式曲线拟合的。然后这个拟合过程所使用的方法叫做 最小二乘法 ,其内在就是构建了一个 函数:让这个函数值最小:
实际上所谓的线性回归 多项式回归具体过程也是和上面差不多的,只是还提供了predict等操作,然后思路要换成机器学习的那种建模说法等。
机器学习中的线性回归会引入更多的数据和更多的特征变量,建模会更加复杂等等,但大体过程也就是类似上面谈及的。
当然这里说一句题外话,虽然很多人对现在的深度学习都抱有这种觉得不过是一种统计学的轻蔑态度,我觉得就过了,正所谓量变到质变,有些东西做的更加复杂之后就和原本那简单的回归是大相径庭的,这里不单单指更加厉害的任意曲线的拟合能力,而是更多的质变在这里面,当然从学习角度这里慢慢去理解是没问题的。
就随机游走问题个人觉得没有继续深究了,下面除了解决计算 $\pi$ 的问题之外,再下面对更多的概率统计知识深入理解之外,再介绍更多的函数拟合和绘图,就差不多该顺理成章转到机器学习那块去了,去建立更多的机器学习模型等,来解决更多实际问题。或者说的更牛掰一些的,模拟和计算世界。
动态规划算法采用分治思想,将某个大问题分解为一些小问题。而贪婪算法对于那些小问题求解局部最优即可,动态规划和朴素解法一样,也是要试着尝试各种组合情况的,所不同的是采用了记忆策略,来将某些类似的子问题一并解决。所以动态规划算法第一,其必须要求子问题有某种类似性;第二,对子问题的解答应用了一种记忆策略。
算法图解的动态规划算法是采用一种网格思路,这对于最长公共子序列问题似乎很适合:
最长公共子序列问题
"""
动态规划法解最长公共子序列问题,经典案例,还是很实用的。
子序列不一定要求递增的,更多的是比较相似度
"""
import pandas as pd
def longest_common_subsequence(seq_one, seq_two):
df = pd.DataFrame(index=[item for item in seq_one], columns=[item for item in seq_two])
df = df.fillna(0)
for i, c1 in enumerate(seq_one):
for j, c2 in enumerate(seq_two):
if c1 == c2:
if (i - 1 < 0) or (j - 1 < 0):
df.iloc[i][j] = 1
else:
df.iloc[i][j] = df.iloc[i - 1][j - 1] + 1
else:
if i < 1 and j < 1:
df.iloc[i][j] = 0
elif i < 1:
df.iloc[i][j] = max(0, df.iloc[i][j - 1])
elif j < 1:
df.iloc[i][j] = max(df.iloc[i - 1][j], 0)
else:
df.iloc[i][j] = max(df.iloc[i - 1][j], df.iloc[i][j - 1])
print(df)
longest_common_subsequence('fort', 'fosh')
longest_common_subsequence('fish', 'fosh')
狄克斯特拉算法
狄克斯特拉算法是用于加权有向图寻找最短路径的算法。所谓加权有向图就是在有向图的基础上每个边增加了权重属性。更确切来说狄克斯特拉算法只适用于加权有向无环图,而且权重不能为负权重。
就加权有向无环图的实现来说当然可以继承自有向无环图,然后再新增一个 weight_data 这个字典值来存储各个边的权重值。定义默认权重值为1。
如下图所示,我们如何找到从1到4的最短路径呢:
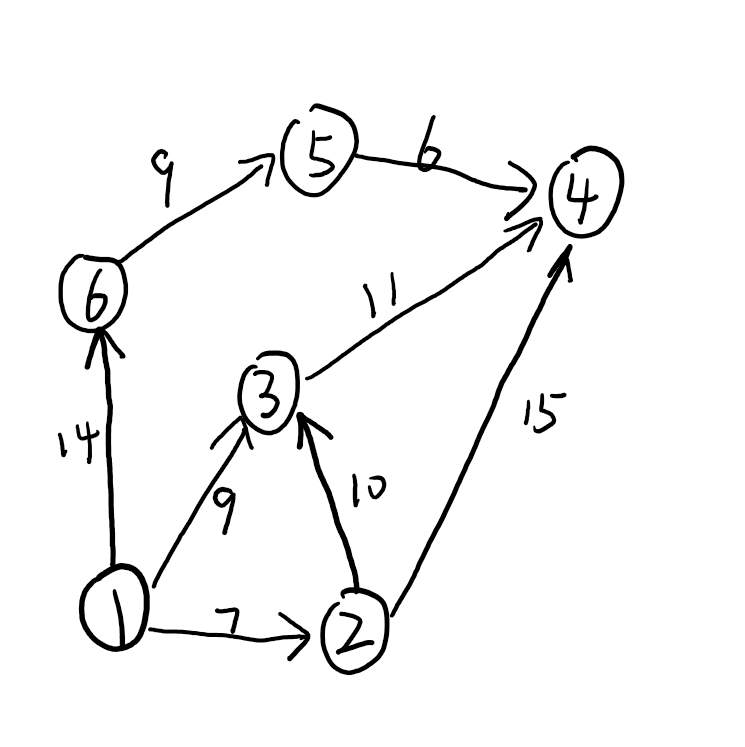
具体狄克斯特拉算法搜索过程用自然语言描述如下:
- 初始化一个costs字典,除了起点为0外,其他都设为infinite。
- 从这个costs字典里面找寻cost最小的顶点
- 计算该顶点下面的子节点的总cost——从起点算起的。如果发现找到了新的路径该路径cost和我们之前记录的costs里面的值相比更小,那么说明我们找到了一个更好的路径。我们这里应该采用一种树结构来记录这个最小路径树,因为这里找到了更好的路径,所以之前的子节点关联的路径应该移除,再插入新的路径。
- 该顶点处理完了记录下来,后面不再处理了。继续从costs里面找cost最小的顶点,继续按照最小cost开销向下扩展。最终我们会得到一个最小路径树。
基本实现
def _init_costs(self, start):
costs = {}
for node in self.nodes():
if node == start:
costs[node] = 0
else:
costs[node] = float("inf")
return costs
@staticmethod
def _find_lowest_cost_node(costs, processed):
"""
start - node the total cost
always return the lowest cost node.
"""
lowest_cost = float("inf")
lowest_cost_node = None
for node, cost in costs.items():
if cost < lowest_cost and node not in processed:
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
def dijkstra_search(self, start):
"""
return the shortest path tree
"""
processed = []
costs = self._init_costs(start)
node = self._find_lowest_cost_node(costs, processed)
spt = Tree(node)
while node is not None:
cost = costs[node]
for sub_node in self.neighbors(node):
new_cost = cost + self.edge_weight((node, sub_node))
if costs[sub_node] > new_cost:
costs[sub_node] = new_cost
if spt.has_node(sub_node):
spt.remove_child(sub_node)
spt.insert_child(node, sub_node)
processed.append(node)
node = self._find_lowest_cost_node(costs, processed)
return spt
狄克斯特拉用更通俗的话语来表述就是逐渐往外扩展所有可能的路径,到某个节点最小cost的路径最终将会被记录下来。
继续到实际的最短路径问题,我们需要加上如下两句来降低程序搜索开销:
......
processed.append(node)
node = self._find_lowest_cost_node(costs, processed)
if node == end:
break
return spt
最终我们利用之前Tree已经写好的 shortest_path_to 方法很容易就得到了最小开销路径:
def dijkstra_shortest_path(self, start, end):
spt = self.dijkstra_shortest_path_search(start, end)
min_path = spt.shortest_path_to(end)
return [i.name for i in min_path]
上面的样例图片情况转成测试代码如下:
graph = WeightedDAG()
graph.add_edge(('1', '3'), 9)
graph.add_edge(('1', '6'), 14)
graph.add_edge(('1', '2'), 7)
graph.add_edge(('2', '3'), 10)
graph.add_edge(('6', '5'), 9)
graph.add_edge(('5', '4'), 6)
graph.add_edge(('3', '4'), 11)
graph.add_edge(('2', '4'), 15)
assert graph.dijkstra_shortest_path('1', '4') == ['1', '3', '4']
Comments !